Základné pojmy

Základné pojmy rastrovej grafiky

Jednou z najdôležitejších úloh počítačovej grafiky je zobrazovanie modelov objektov zo spojitého priestoru $E^3$ do dvojrozmerného diskrétneho priestoru, ktorý predstavuje obrazovka počítača. [6]

Prakticky všetky súčasné grafické displeje používajú metódu rastrového skenovania.

Jej podstata spočíva v tom, že počítačový program pripravuje celý obraz v pamäťovom bufri (frame buffer) nazývanom aj bitmapa, pričom operuje s diskrétnymi bodmi. Aj samotný obraz pozostáva z tzv. obrazovkových bodov známych ako pixely (picture elements), ktoré môžu byť zapnuté alebo vypnuté. Pixel je najmenší adresovateľný element obrazovky, jej najmenšia časť, ktorú môžeme nezávisle ovládať, čiže môžeme jej priradiť napríklad určitú farbu príp. odtieň - hodnotu šedej, ak zariadenie je monochromatické. Také jednoduché útvary, akými sú napr. krivky, špeciálne úsečky, potom zobrazujeme tak, že rozsvietime určitou intenzitou (jasom) reťazec pixlov medzi jej začiatočným a koncovým bodom. Dôležitú úlohu pri tvorbe obrazov dvoj a viac-rozmerných útvarov hrá vypĺňanie oblastí takýmito pixlami. Keďže pixely nie sú ideálne geometrické body, ale isté podmnožiny (najčastejšie štvorčeky) konečnej roviny, netvoria takto skonštruované objekty krivky, úsečky, mnohouholníky v matematickom zmysle slova, ale my ich budeme za krivky, úsečky resp. mnohouholníky považovať, pričom sa budeme snažiť, aby sa im čo najviac podobali. Ako sme povedali vyššie, každému pixlu je v bitmape priradené určité číslo špecifikujúce jeho farbu, odtieň šedej a pod. Z praktických dôvodov je užitočné predstavovať si obrazovku ako pravouholníkovú mriežku, ktorá má $r$ riadkov očíslovaných zdola nahor nezápornými celými číslami $0,1,..., r -1$ a $s$ stĺpcov očíslovaných zľava doprava číslami $0,1,..., s -1$. Potom každý pixel bude jednoznačne určený dvojicou tzv. obrazovkových súradníc $(x, y)\in \lbrace 0,1,..., r -1\rbrace \times\lbrace 0,1,..., s -1\rbrace$ (Obr. 1). [6]

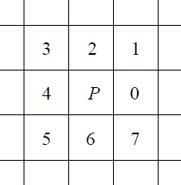
Na druhej strane bitmapa býva uložená v pamäti počítača ako jednorozmerné pole, ktorého indexy i $\in \lbrace 0,1,..., r \times s -1 \rbrace$ sú také, že pixlu $(x,y)$ priradia index $i =x+ys$. Napr. pre $r=5$ a $s=7$ je všetkých pixlov $35$ a pixlu $(5,3)$ prislúcha $i=5+3.7=26$. Na Obr. 1 je ilustrované vzájomne jednoznačné priradenie medzi množinou pixlov a frame bufrom (bitmapou). [6]

Obr. 1 - Bitmapa [6]

Obrazovka s rozlíšiteľnosťou napr. $512 \times 512$ pixlov sa skladá z $512^2=262144$ pixelov uložených do $512$ riadkov a $512$ stĺpcov očíslovaných číslami $0,1,…,511$. Tie vytvárajú množinu usporiadaných dvojíc nezáporných celých čísel ${0,1,...,511}\times {0,1,...,511}$, ktorá sa nazýva súradnicovým priestorom obrazovky – alebo DC priestorom (Device Coordinates Space). Ak by aplikačný program pracoval len v malých celočíselných používateľských súradniciach, mohli by sme tento priestor považovať za vyhovujúci pracovný priestor pre počítačovú grafiku. Existujúce grafické systémy však nemôžu aplikačné programy takto obmedzovať, a preto je potrebné, aby DC-priestor akceptoval aj reálne súradnice. Treba ho teda rozšíriť na priestor reálnych súradníc a to tak, aby pixely zodpovedali práve tým bodom rozšíreného DC, ktoré majú celočíselné súradnice. Toto možno dosiahnuť napr. tak, že ideálnemu bodu obrazovky s reálnymi súradnicami $(x, y)$; $x\geq 0$, $y\geq0$ priradíme pixel so súradnicami (round(x),round(y)), kde napríklad: $round(x) = k \Rightarrow$ ak $k$ je to jediné nezáporné celé číslo, pre ktoré platí: $x \in \langle k-0.5, k+0.5)$.

Pripomenieme ešte, že dĺžky na obrazovke sa nemerajú v cm ani v palcoch, ale v pixloch, čo predstavuje dĺžku jednej strany pixla. Keďže každému ideálnemu bodu $(x,y)$; $x, y \in $ $\mathbb{R}$ (presnejšie z istej podmnožiny $\mathbb{R}$) vieme jednoznačne priradiť pixel a pixlu miesto vo frame bufri, prislúcha toto miesto aj bodu $(x,y)$. [6]

Bitová mapa je teda časť pamäte počítača, ktorú si predstavme ako štvorcovú sieť. Jednotlivé jej prvky zodpovedajú obrazovým bodom na rastrovom zariadení. Ak je v niektorom prvku bitovej mapy zapísaná hodnota, tak je príslušný pixel rastra vysvietený farbou prislúchajúcou tejto hodnote. Pri vykresľovaní úsečky sa pre vykreslenie jednotlivých bodov volá funkcia, ktorá na určené miesto bitovej mapy zapíše hodnotu farby.

V niektorých algoritmoch vypĺňania budeme potrebovať pojem susednosť.

V bitovej mape má každý vnútorný bod ôsmich susedov. Je zvykom označovať ich spôsobom, ako je uvedené na Obr. 2. Susedov s číslami 0, 2, 4, 6 nazývame priami susedia, alebo 4-susedia, susedov s číslami 1, 3, 5, 7 nazývame nepriami susedia. Všetkých spolu nazývame 8-susedia.

Obr. 2 - Susednosť v bitovej mape [6]

Oblasť je množina prvkov bitovej mapy, ktoré sú súvislo pospájané. Prvkom oblasti hovoríme aj body. Oblasti môžu byť zadané všetkými svojimi bodmi (používa sa aj pojem vnútorne definovaná oblasť) je zadaná farba týchto bodov a typ súvislosti. Pri oblasti danej hranicou je zadaná farba hranice.

Podľa typu súvislosti rozdeľujeme oblasti na:

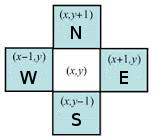
  • 4-súvislé (4-connected): Oblasť, ktorej každé dva prvky môžeme spojiť postupnosťou 4-susedov. Sused sa teda môže nachádza iba vo vodorovnom alebo zvislom smere. Smery označujeme pomocou skratiek N, S, E, W (z ang. North - Sever, South - Juh, East - Východ, West - Západ) (Obr. 3).
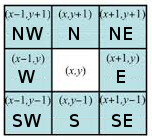
  • 8-súvislé (8-connected): Oblasť, ktorej každé dva prvky môžeme spojiť postupnosťou 8-susedov, teda najbližší sused každého pixla môže ležať v ôsmich okolitých smeroch. Tieto smery označujeme pomocou skratiek N, S, E, W, NE, SE, SW, NW (z ang. Northeast - Severovýchod, Southeast - Juhovýchod, Southwest - Juhozápad, Northwest - Severozápad). 8-susednosť sa využíva aj pri algoritmoch vyplňovania oblastí (Obr. 4).

Je zrejmé, že každá 4-súvislá množina je 8-súvislá, ale naopak to neplatí.

Obr. 3 - 8 susednosť pixelov
Obr. 4 - 4 susednosť pixelov

Dvojrozmerné geometrické transformácie

Keďže téma transformácie je dobre spracovaná v použitej slovenskej literatúre, v tejto podkapitole čerpáme informácie z [1].

V úlohách často vytvárame alebo používame obraz určitého objektu, ktorý treba vhodne transformovať, teda vybrať určitú časť a prepočítať súradnice na dané výstupné zariadenie. V tejto podkapitole si ukážeme stručne vzájomnú súvislosť medzi maticami a lineárnymi transformáciami v rovine a odvodíme matice najčastejšie používaných rovinných transformácií: posunutia, otočenia a škálovania.

Medzi transformáciami a maticami je vzťah: každej lineárnej transformácií vieme priradiť určitý typ matice. Pri lineárnych transformáciách dvojrozmerných vektorových priestorov používame maticu typu 2x2.

Každý bod v rovine budeme stotožňovať s vektorom typu 1x2. Pri vyjadrovaní bodov pomocou matíc 1x3 hovoríme o homogénnych súradniciach. Bodu so súradnicami $(x,y)$ priradíme homogénnu súradnicu $(x,y,1)$ a vektoru so súradnicami $(x,y)$ priradíme $(x,y,0)$.


Otočenie alebo rotácia

Transformácia objektu po kruhovej dráhe sa nazýva otočenie.

Je určené uhlom a stredom otočenia (pevným bodom). Príklad na Obr. 5 ukazuje otočenie objektu so stredom v začiatku. súradnicovej sústavy o uhol 15 stupňov.

Obr. 5 - Otočenie pre daný objekt [1]

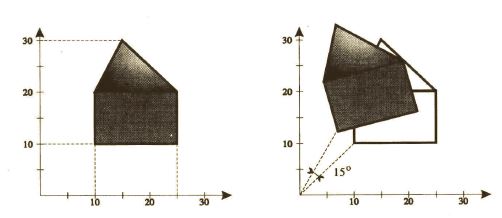
Odvodíme vzťah pre vyjadrenie tohto zobrazenia. Objekt môžeme otočiť o ľubovolný uhol $\varphi$ vzhľadom k začiatku súradnicovej sústavy. Keďže sa všetky body otočia zhodne, stačí ukázať, čo sa deje s ľubovoľne vybratým bodom.

Pri otočení o uhol $\varphi$ sa bod $A(x,y)$ zobrazí do bodu $A(x',y')$ (Obr. 6).

Obr. 6 - Otočenie bodu $A$ do bodu $A'$ [1]

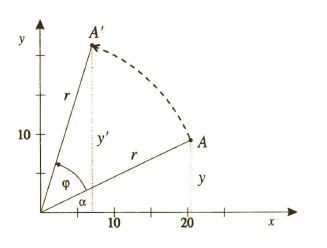
Použijeme polárne súradnice bodov:

\begin{align*} x=r.cos(\alpha) && x'=r.cos(\alpha + \varphi)\\ y=r.sin(\alpha) && y'=r.sin(\alpha + \varphi) \end{align*}

Pomocou súčtu uhlov pre goniometrické funkcie $sin(\alpha + \varphi)$ a $cos(\alpha + \varphi)$ môžeme vyjadriť $x'$ a $y'$ ako

\begin{equation*} \begin{split} x'=r.cos(\alpha).cos(\varphi)-r.sin(\alpha).sin(\varphi) =x.cos(\varphi)-y.sin(\varphi)\\ y'=r.cos(\alpha).sin(\varphi)+r.sin(\alpha).cos(\varphi) =x.sin(\varphi)+y.cos(\varphi) \end{split} \end{equation*}

Tým sme dostali transformačnú maticu $R$ otočenia o uhol $\varphi$ v homogénnych súradniciach:

\begin{equation*} R= \begin{pmatrix} cos(\varphi) & sin(\varphi) & 0\\ -sin(\varphi) & cos(\varphi) & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}

Škálovanie alebo zmena mierky

Pomocou tejto transformácie môžeme zmeniť veľkosť objektu. Tento typ zobrazenia všeobecne môžeme zapísať nasledovne: \begin{equation*} \begin{split} x'=s_x.x\\ y'=s_y.y \end{split} \end{equation*} kde $s_x$ a $s_y$ sa nazývajú škálovacie faktory a zodpovedajúca transformačná matica $S$ má tvar:

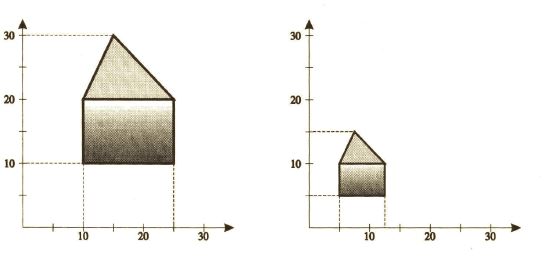
\begin{equation*} S= \begin{pmatrix} s_x & 0 & 0\\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}

Pre škálovanie vždy existuje pevný bod, v našom prípade nech je to začiatok súradnicovej sústavy. Na Obr. 7 vidíme škálovanie objektu v tvare domčeka pre hodnoty $s_x=0.5$ a $s_y=0.5$.

Obr. 7 - Škálovanie objektu [1]

Posunutie objektu a sústavy súradníc

Posunutie je premiestnenie objektu z jednej pozície do druhej.

Na rozdiel od rotácie a škálovania nemá pevný bod. Posunutie v rovine je definované pomocou vektora $(t_x, t_y)$. Zodpovedajúcu transformačnú maticu $T$ môžeme zapísať nasledovne:

\begin{equation*} T= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ t_x & t_y & 1 \end{pmatrix} \end{equation*}

Ale ako sa zmenia súradnice bodov pri posunutí sústavy súradníc?

Na Obr. 8 vidíme, že ten istý bod má vzhľadom k posunutej sústave súradníc súradnice posunuté o opačný vektor $(-t_x, -t_y)$.

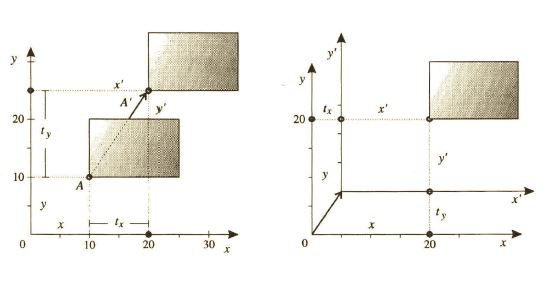
Obr. 8 - Posunutie bodu a sústavy súradníc [1]

Zodpovedajúca matica $T'$ má potom tvar:

\begin{equation*} T'= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ -t_x & -t_y & 1 \end{pmatrix} \end{equation*}

Matica $T'$ je inverzná k matici posunutia $T$. Obdobne vieme odvodiť inverzné matice pre škálovanie a otočenie sústavy súradníc ako:

\begin{equation*} S'= \begin{pmatrix} \frac{1}{s_x} & 0 & 0\\ 0 & \frac{1}{s_y} & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*} \begin{equation*} R'= \begin{pmatrix} cos(\varphi) & -sin(\varphi) & 0\\ sin(\varphi) & cos(\varphi) & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}

Všeobecne platí že pre transformáciu objektov a transformáciu súradnicovej sústavy platí vzťah navzájom inverzného zobrazenia, pokiaľ sú tieto zobrazenia jednoznačné.


Súmernosti podľa priamky

Niektoré aplikácie počítačovej grafiky vyžadujú aj iné transformácie v rovine. V prípade, že uvažujeme len transformácie zachovávajúce začiatok sústavy súradníc, potom môžeme napísať matice pre súmernosti(zrkadlenia) podľa osi $x$ a $y$.

\begin{equation*} Z_x= \begin{pmatrix} 1 & 0 & 0\\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*} \begin{equation*} Z_y= \begin{pmatrix} -1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}

Ide o špeciálny prípad škálovania, kde $s_x=-1$ alebo $s_y=-1$.

V obidvoch prípadoch transformácie menia orientáciu (Obr. 9). Na toto treba dávať pozor. Ak totiž máme mnohouholník orientovaný proti smeru chodu ručičiek, potom takáto transformácia zmení orientáciu mnohouholníka na opačnú. Maticu súmernosti podľa ľubovolnej priamky získame skladaním s príslušnými otočeniami a základnými súmernosťami podľa osí.

Obr. 9 - Súmernosti podľa osi $x$ a $y$ [1]

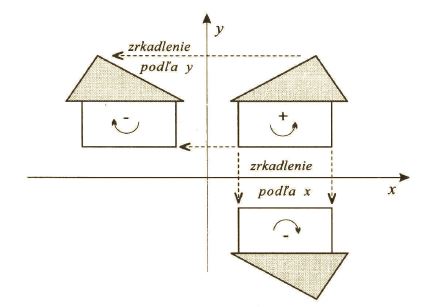
Skosenie

Tento typ animácie vyvoláva dojem, akoby sa objekty po vrstvách posúvali.

Rozoznávame dva typy:

  • skosenie v smere $x$, kde sa mení spradnica $x$ a súradnica $y$ zostáva nezmenená
  • skosenie v smere $y$, kde sa mení spradnica $y$ a súradnica $x$ zostáva nezmenená

Obidva typy majú jednoduchú transformačnú maticu:

\begin{equation*} S_x= \begin{pmatrix} 1 & 0 & 0\\ s_x & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*} \begin{equation*} S_y= \begin{pmatrix} 1 & s_y & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}

Na nasledujúcom obrázku vidíme, ako pôsobí skosenie na jednoduchý objekt.

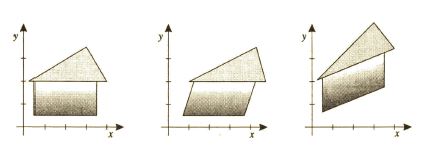
Obr. 10 - Skosenie podľa $x$ ($s_x$=0.4) a $y$ ($s_y$=0.4) [1]

Zloženie dvojrozmerných transformácií

Ukážeme, ako môžeme využiť násobenie matíc pri skladaní zobrazení na príklade.

Chceme vyjadriť zmenu mierky so stredom v ľubovoľnom pevnom bode $A(x,y)$. Riešime to tak, že uskutočníme za sebou tri zobrazenia, a to:

  1. Posunieme sústavu súradníc do bodu $A$.
  2. Uskutočníme zmenu mierky v začiatku súradnicovej sústavy.
  3. Posunieme späť bod $A$ do pôvodného začiatku.

Každej tejto transformácií zodpovedá jedna transformačná matica. Výslednej zloženej transformácii zodpovedá nasledujúca matica:

\begin{equation*} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -x & -y & 1 \\ \end{pmatrix} * \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} * \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x & y & 1 \\ \end{pmatrix} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ x(1-s_x) & y(1- s_y) & 1 \\ \end{pmatrix} \end{equation*}

Podobne otočenie zo stredom v ľubovoľnom bode $A(x,y)$ vykonáme pomocou týchto troch transformácií:

  1. Posunieme sústavu súradníc do bodu $A$.
  2. Uskutočníme otočenie okolo začiatku súradnicovej sústavy o uhol $\varphi$.
  3. Posunieme späť bod $A$ do pôvodného začiatku.

Výslednú zloženú transformáciu vyjadríme ako:

\begin{equation*} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -x & -y & 1 \\ \end{pmatrix} * \begin{pmatrix} cos(\varphi) & sin(\varphi) & 0\\ -sin(\varphi) & cos(\varphi) & 0 \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x & y & 1 \\ \end{pmatrix} = \end{equation*} \begin{equation*} \begin{pmatrix} cos(\varphi) & sin(\varphi) & 0 \\ -sin(\varphi) & cos(\varphi) & 0 \\ x(1-cos(\varphi))+ysin(\varphi) & y(1- cos(\varphi))-xsin(\varphi) & 1 \\ \end{pmatrix} \end{equation*}