Vypĺňanie
V počítačovej grafike v mnohých prípadoch nie je potrebné vykresliť jedinú priamku alebo krivku, ale vyplniť určitú oblasť.
V niektorých algoritmoch sa pri hľadaní a následnom vypĺňaní pixlov predpokladá, že poznáme aspoň jeden vnútorný bod v súvislej oblasti - semienko. Takýto typ vypĺňania sa preto nazýva semienkové vypĺňanie
Pri vypĺňaní prechádzajú algoritmy všetkými pixlami súvislej oblasti a farbia ich farbou, ktorou sa má táto oblasť zafarbiť (tzv. nová farba).
Body 4- alebo 8-susedných oblastí klasifikujeme takto:
- Testovaný bod je vnútorný, ak má inú farbu ako hraničný. Vypĺňanie založené na tomto princípe sa nazýva hraničné vypĺňanie (po hranicu).
- Testovaný bod je vnútorný, pokiaľ má farbu, ktorou sú zafarbené všetky body vnútra. Toto je charakteristické pre tzv. záplavové / lavínové vypĺňanie, pri ktorom sa súvislá oblasť prefarbuje novou farbou (všetky jej pixle tou istou).
- Testovaný bod je vnútorný, ak má farbu, ktorá sa výrazne líši od farby hranice. Je to špeciálny prípad hraničného vypĺňania, v prípade, že hranica má len približne určený farebný odtieň a jas, čo býva obyčajne dôsledkom vyhladzovania obrazu a špeciálne hranice. V tomto prípade hovoríme o mäkkom vypĺňaní.
Vo všeobecnosti existujú dve možnosti pre definovanie oblasti, ktorá sa má vyplniť: oblasť zadaná svojimi vnútornými bodmi alebo oblasť zadaná hranicou.
Intuitívny prístup, ktorý nás napadne, je chápať zadanú množinu hraničných pixlov ako pre hranicu určitej oblasti, podobne ako je to s bodmi uzavretej krivky v rovine. Takáto množina pixlov by mala byť súvislá a podobne ako uzavretá rovinná krivka by mala rozdeľovať nekonečnú mriežku na dve časti: vnútro a vonkajšok.
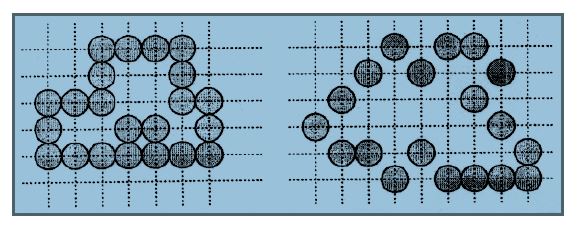
Podľa známej Jordanovej vety platí, že každá uzavretá krivka v rovine rozdeľuje rovinu na dve súvislé oblasti: vnútro a vonkajšok. Zatiaľ však nemáme definované, čo sa rozumie uzavretou krivkou v našom prípade, dokonca nám bez tejto definície môžu nastať určité problémy (Obr. 1).
Ak hraničná krivka je 8-súvislá, tak vo všeobecnosti neplatí, že rozdeľuje nekonečnú sieť do dvoch 8-súvislých oblastí, pretože (ako vidieť na Obr. 1) vnútro a vonkajšok sa dajú navzájom spojiť 8-súvislou cestou. Existuje však zaujímavý spôsob, ako upraviť tento problém. Špeciálne, ak požadujeme, aby hraničná krivka bola 8-súvislá, tak je potrebné, aby ňou definovaná oblasť bola 4-súvislá. Podobne, ak chceme, aby hranica bola 4-súvislá, je vhodné požadovať, aby oblasť, ktorú definuje, bola 8-súvislá.
Jeden zo základných úloh počítačovej grafiky je určenie vnútorného bodu mnohouholníka.
Na objasnenie pojmov ako sú vnútro alebo vonkajšok mnohouholníka si uvedieme základné definície z [8].
Okolie bodu je každá otvorená množina obsahujúca daný bod.
Bod $A$ priestoru $X \subset E^{n}$ je vnútorný bod množiny M$\subset$X, ak existuje jeho okolie ležiace v M. Množina všetkých vnútorných bodov množiny M sa nazýva vnútro množiny M a označuje sa int$M$(z angl. interior = vnútro).
Bod $A$ je hraničný bod množiny M, ak každé jeho okolie pretína množinu M aj jej doplnok (t.j. obsahuje bod patriaci množine M aj bod jej nepatriaci). Množina všetkých hraničných bodov množiny M sa nazýva hranica množiny M a označuje sa $\partial$M alebo bd$M$.
Bod $A$ je vonkajší bod množiny M, ak existuje jeho okolie nepretínajúce množinu M. Množina všetkých vonkajších bodov množiny M sa nazýva vonkajšok množiny M a označuje sa ext$M$ (z angl. exterior = vonkajšok).
Platí, že bod je vnútorným bodom mnohouholníka, ak polpriamka rovnobežná s osou $x$ vychádzajúca z tohto bodu pretne mnohouholník v nepárnom počte hrán [1]. Predpokladáme pri tom, že polpriamka neprechádza žiadnym vrcholom mnohouholníka. Ak by takáto situácia nastala, môžeme mnohouholník posúvať.
V tejto kapitole si uvedieme tri algoritmy pre vypĺňanie a pre oblasť danú hranicou uvedieme jeden vylepšený algoritmus. Ten ukáže, ako môžeme rozložiť mnohouholník do rastra.