Počítačová grafika

Bresenhamov stredový elipsový algoritmus (Midpoint Ellipse Algorithm)

Princíp algoritmu

Bresenhamov stredový elipsový algoritmus je založený na rovnakom princípe ako Bresenhamov kružnicový algoritmus. Dané sú parametre $r_x,r_y$ a stred elipsy $(x_C,y_C)$. Vyčísľujeme body elipsy v základnej pozícii a to so stredom v bode $(0,0)$. Následne sa všetky body elipsy posunú tak, že bod $(x_C,y_C)$ je jej stredom.

Ak chceme vykresliť elipsu v inej ako základnej polohe (ak hlavná a vedľajšia os elipsy nie sú rovnobežné so súradnicovými osami), môžeme elipsu otočiť okolo tredu otáčania (viď Kapitola - rotácia).

V nasledujúcej časti ukážeme rasterizáciu elipsy so stredom v bode $(0,0)$ a základnej pozícii. Algoritmus budeme aplikovať v I. kvadrante v dvoch oblastiach (Obr. 1). Tieto oblasti vzniknú rozdelením I. kvadrantu na dva v bode elipsy, v ktorom dotyčnica k elipse má smernicu $m=-1$.

Hranicou medzi oblasťami je priamka spájajúca stred elipsy s dotykovým bodom.

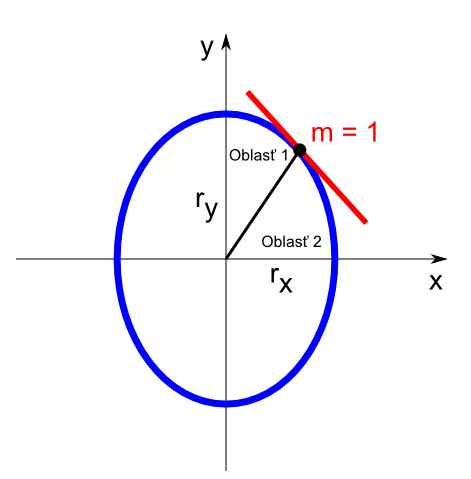
Začíname v bode elipsy $(0,r_y)$ a postupujeme v smere chodu hodinových ručičiek. Najprv postupujeme jednotkovým krokom v smere osi $x$ v prvej oblasti, až pokým sa nedostaneme na hranicu medzi oblasťami. Vtedy prejdeme na jednotkový krok v smere osi $y$, až kým neprejdeme celý I. kvadrant.Tento postup je potrebný, pretože ak by sme postupovali jednotkovým krokom iba v smere jednej zo súradnicových osí, pri rasterizácii by vznikali medzery medzi zobrazenými pixlami a výsledná elipsa by bola nespojitá.

Pre smernicu $m$ dotyčnice v bode elipsy $X=(x,y)$ na hranici oblasti platí $m=-1 \Rightarrow \frac{dy}{dx}=\frac{2r_y^2x}{2r_x^2y} \Rightarrow 2r_y^2x=2r_x^2y$. Teda pre smernicu $m$ dotyčnice v bode elipsy $X=(x,y)$ v prvej oblasti I. kvadrantu platí $m>-1$ a v druhom $m \lt -1$. Preto môžeme povedať, že bod elipsy $X=(x,y)$ sa nachádza v prvej oblasti, ak platí $2r_y^2x \geq 2r_x^2y$, t.j. vzorkujeme jednotkovým krokom v smere osi $x$, inak v smere osi $y$.

Samozrejme, modifikáciou algoritmu je možné postupovať zo začiatočného bodu $(r_x,0)$ proti smeru hodinových ručičiek.

Zapíšeme rovnicu elipsy vyjadrenú v rovnici elipsy stredom $(x_C,y_C)=(0,0)$ ako $f(x,y)=r_y^2x^2+r_x^2y^2-r_x^2r_y^2$.

Je zrejmé, že platí:

• Ak $f(x,y) \lt 0$ tak bod $X=(x,y)$ je vnútorný bod elipsy
• Ak $f(x,y)=0$ tak bod $X=(x,y)$ je bodom elipsy
• Ak $f(x,y) \gt 0$ tak bod $X=(x,y)$ je vonkajším bodom elipsy

Napr. nachádzame sa v bode elipsy $(x_i,y_i)$ a rozhodujeme sa, ktorý z nasledujúcich bodov pozdĺž elipsy vykreslíme. Môžu nastať dve situácie:

1. Nachádzame sa v prvej oblasti. Teda platí $2r_y^{2}x_i\leq 2r_x^{2}y_i$ a kandidáti na nasledujúci bod sú body na mieste $E=(x_i+1,y_i)$ a $SE=(x_i+1,y_i-1)$ (Obr. 2).

   

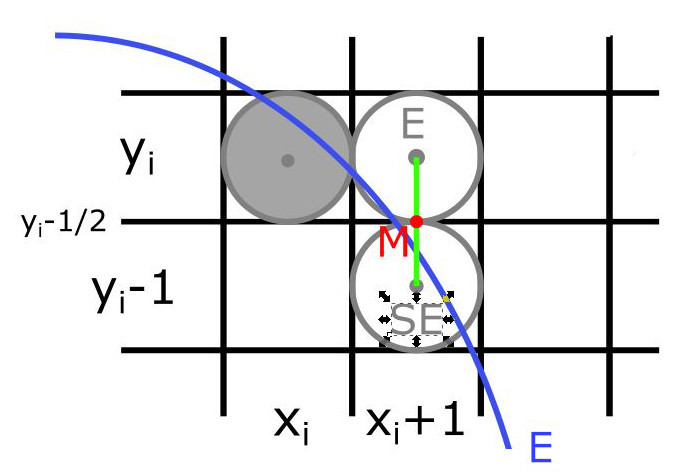
   Ako v oboch Midpoint algoritmoch, použijeme bod $M=stred(E,SE)=(x_i+1,y_i-\frac{1}{2})$. Vyjadríme si rozhodovací parameter pre prvú oblasť ako $p1_i=f(M)=f(x_i+1,y_i-\frac{1}{2})=r_y^2(x_i+1)^2+r_x^2(y_i-\frac{1}{2})^2-r_x^2r_y^2$ a odvodíme rekurentný vzorec. $p1_{i+1}=f(x_{i+1}+1,y_{i+1}-\frac{1}{2})=r_y^2\left(x_{i+1}+1 \right)^2+r_x^2\left(y_{i+1}-\frac{1}{2} \right)^2 -r_x^2r_y^2 $.

   Z toho $p1_{i+1}=p1_i+2r_y^2(x_i+1)+r_y^2$ +$r_x^2\left((y_{i+1}-\frac{1}{2})^2-(y_i-\frac{1}{2})^2\right)$.

   Zrejme platí:

   • Ak $p1_i \lt 0$, tak vyberáme za nasledujúci pixel $(x_{i+1},y_{i+1})=E=(x_i+1,y_i)$ a $p1_{i+1}=p1_i+2r_y^2x_{i+1}+r_y^2$.
   • Ak $p1_i\geq 0$, tak vyberáme za nasledujúci pixel $(x_{i+1},y_{i+1})=SE=(x_i+1,y_i-1)$ a $p1_{i+1}=p1_i+2r_y^2x_{i+1}+r_y^2-2r_x^2y_{i+1}$.

   Potrebujeme ešte vyčísliť hodnotu začiatočného parametra v začiatočnej pozícii pre $(x_0,y_0)=(0,r_y)$, teda $p1_0=f(1,r_y-\frac{1}{2})=r_y^2-r_x^2r_y+\frac{1}{4} r_x^2$

2. Ak $2r_y^{2}x_i\geq 2r_x^{2}y_i$ nachádzame sa v druhej oblasti. Teda kandidáti na nasledujúci bod sú body na mieste $S=(x_i,y_i-1)$ a $SE=(x_i+1,y_i-1)$ (Obr. 3).

   V tomto prípade použijeme bod $M=stred(S,SE)=(x_i+\frac{1}{2},y_i-1)$.

   

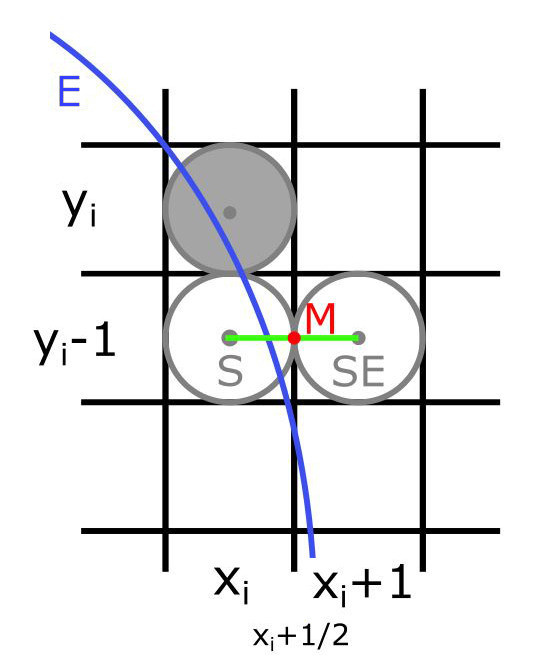
   Vyjadríme si rozhodovací parameter pre druhú oblasť ako $p2_i=f(M)=f(x_i+\frac{1}{2},y_i-1)=r_y^2(x_i+\frac{1}{2})+r_x^2(y_i-1)-r_x^2r_y^2$ a odvodíme rekurentný vzorec. $p2_{i+1}=f(x_{i+1}+\frac{1}{2},y_{i+1}-1)=r_y^2(x_{i+1}+\frac{1}{2})^2+r_x^2\left(y_i-1 \right)^2 -r_x^2r_y^2 $. Z toho $p2_{i+1}=p2_i+2r_x^2(y_i-1)+r_x^2+r_y^2\left((x_{i+1}+\frac{1}{2})^2-(x_i+\frac{1}{2})^2\right)$.

   Zrejme platí:

   • Ak $p2_i \lt 0$, tak vyberáme za nasledujúci pixel $(x_{i+1},y_{i+1})=S=(x_i,y_i-1)$ a $p2_{i+1}=p2_i-2r_x^{2}y_{i+1}+r_x^{2}$.
   • Ak $p2_i\geq 0$, tak vyberáme za nasledujúci pixel $(x_{i+1},y_{i+1})=SE=(x_i+1,y_i-1)$ a $p2_{i+1}=p2_i+2r_y^{2}x_{i+1}-2r_x^{2}y_{i+1}+r_x^{2}$.

   Potrebujeme ešte vyčísliť hodnotu začiatočného parametra v poslednom bode z prvej oblasti, ktorý je vlastne bod $(x_0,y_0)$ v oblasti dva. Teda $p2_0=f(x_0+\frac{1}{2},y_0-1)=r_y^2(x_0+\frac{1}{2})^2+r_x^2(y_0-1)^2-r_x^2r_y^2$.

   Pre zjednodušenie môžeme pixely v druhej oblasti I kvadrantu vyčísľovať taktiež z bodu $(r_x,0)$ proti smeru chodu hodinových ručičiek, až kým sa nedostaneme do posledného vyčísleného bodu prvej oblasti.

Tak ako v kružnicovom algoritme, pri výpočte $p1_{i+1}$ a $p2_{i+1}$ používame iba operácie sčitovania a odčitovania. Hodnoty $2r_y^{2}x_{i+1}$ a $2r_x^{2}y_{i+1}$ je možno počítať s pomocou konštantného prírastku. Pre hodnotu začiatočného parametra v bode $(x_0,y_0)=(0, r_y)$ platí $2r_y^{2}x_0=0$ a $2r_x^{2}y_0=2r_x^{2}r_y$. Ako sa budú hodnoty $x_i$ a $y_i$ zvyšovať, budú sa tieto parametre meniť v I. kvadrante takto:

• Ak $x_{i+1} \gt x{i}$ platí $2r_y^{2}x_{i+1}=2r_y^{2}x_i+2r_y^{2}$, inak $2r_y^{2}x_{i+1}=2r_y^{2}x_i$.
• Ak $y_{i+1} \lt y{i}$ platí $2r_x^{2}y_{i+1}=2r_x^{2}x_i-2r_x^{2}$, inak $2r_x^{2}y_{i+1}=2r_x^{2}y_i$.

Potom pre začiatočnú hodnotu $p_0$ v bode $(x_C,y_C)=(0,r)$ dostaneme $p_0=3-2r$. Hoci pri výpočte parametra sa používa násobenie, príslušný násobok je druhou mocninou a je možná implementácia cez logické operácie. Ostatné operácie sú celočíselné sčítanie a odčítanie.

Postup výpočtu

Kroky algoritmu vieme zhrnúť nasledovne:

1. Zadaj $r_x$ a $r_y$ a stred elipsy $(x_C,y_C)$ a urči prvý bod na elipse so stredom v začiatku $(x_0 ,y_0)=(0, r_y)$.
2. Vypočítaj začiatočnú hodnotu rozhodovacieho parametra v prvej oblasti ako $p1_0=r_y^{2}-r_x^{2}r_y+\frac{1}{4}r_x^{2}$, urči $2r_y^2x_0 a 2r_x^2y_0$.

3. V každej pozícii $x_i$ v prvej oblasti, štartujúc v $i=0$, vykonaj nasledujúci test:

   1. Ak $p1_i \lt 0$: nasledujúci bod pozdĺž elipsy so stredom $(0,0)$ bude $(x_{i+1}, y_{i+1})=(x_i+1,y_i)$ a $p1_{i+1}=p1_i+2r_y^{2}x_{i+1}+r_y^{2}$.
   2. Inak je nasledujúci bod $(x_{i+1}, y_{i+1})=(x_i+1,y_i-1)$ a $p1_{i+1}=p1_i+2r_y^{2}x_{i+1}-2r_x^{2}y_{i+1}+r_y^{2}$.
   a urči $2r_y^{2}x_{i+1}=2r_y^{2}x_i+2r_y^{2}$ a $2r_x^{2}y_{i+1}=2r_x^{2}y_i-2r_x^{2}$
4. Opakuj krok 3. až pokým $2r_y^{2}x\leq 2r_x^{2}y$.
5. Urči začiatočnú hodnotu rozhodovacieho parametra v druhej oblasti využitím posledného bodu z prvej oblasti ako $p2_0=r_y^{2}(x_0+\frac{1}{2})^{2}+r_x^{2}(y_0-1)^{2}-r_x^{2}r_y^{2}$
6. V každej pozícii $x_i$ v druhej oblasti, štartujúc v $i=0$, vykonaj nasledujúci test:
   1. Ak $p2_i \gt 0$: nasledujúci bod pozdĺž elipsy so stredom $(0,0)$ bude $(x_{i+1}, y_{i+1})=(x_i,y_i-1)$ a $p2_{i+1}=p2_i-2r_x^{2}y_{i+1}+r_x^{2}$.
   2. Inak je nasledujúci bod $(x_{i+1}, y_{i+1})=(x_i+1,y_i-1)$ a $p2_{i+1}=p2_i+2r_y^{2}x_{i+1}-2r_x^{2}y_{i+1}+r_x^{2}$.
   a urči $2r_y^{2}x_{i+1}=2r_y^{2}x_i+2r_y^{2}$ a $2r_x^{2}y_{i+1}=2r_x^{2}y_i-2r_x^{2}$.
7. Urči súmerné body v ostatných troch kvadrantoch.
8. Posuň každú vypočítanú pixlovú pozíciu $(x, y)$ na elipsu so stredom $(x_C ,y_C )$ a zobraz bod so súradnicami: $x=x+x_C$,$y=y+y_C$.

Príklad

Na ilustráciu algoritmu si ukážeme rasterizáciu elipsy s parametrami $r_x=8$ a $r_y=6$ a stredom elipsy v bode $(0,7)$

1. $(x_0,y_0)=(0,r_y)=(0,6)$.
2. $p1_0=-332$, $2r_y^2x_0=0$ a $2r_x^2y_0=2.8^2.6=768$. Výraz $2r_y^2x$ sa bude zvyšovať o hodnotu $2r_y^2=72$ a výraz $2r_x^2y$ o hodnotu $-2r_x^2=-128$.
3. • $i=0:$ $p1_0 \lt 0 \Rightarrow (x_1,y_1)=(x_0+1,y_0)=(1,6)$, $p1_1=p1_0+2r_y^2x_1+r_y^2=-224$, $2r_y^2x_1=72$ a $2r_x^2y_1=768$.
   • $i=1:$ $p1_1 \lt 0 \Rightarrow (x_2,y_2)=(x_1+1,y_1)=(2,6)$, $p1_2=p1_1+2r_y^2x_2+r_y^2=-44$, $2r_y^2x_2=72+72=144$ a $2r_x^2y_2=768$.
   • $i=2:$ $p1_2 \lt 0 \Rightarrow (x_3,y_3)=(x_2+1,y_2)=(3,6)$, $p1_3=p1_2+2r_y^2x_3+r_y^2=208$, $2r_y^2x_3=144+72=216$ a $2r_x^2y_3=768$.
   • $i=3:$ $p1_3 \gt 0 \Rightarrow (x_4,y_4)=(x_3+1,y_3-1)=(4,5)$, $p1_4=p1_3+2r_y^2x_4-2r_x^2y_4+r_y^2=-108$, $2r_y^2x_4=216+72=288$ a $2r_x^2y_4=768-128=640$.
   • $i=4:$ $p1_4 \lt 0 \Rightarrow (x_5,y_5)=(x_4+1,y_4)=(5,5)$, $p1_5=p1_4+2r_y^2x_5+r_y^2=288$, $2r_y^2x_5=288+72=360$ a $2r_x^2y_5=640$.
   • $i=5:$ $p1_5 \gt 0 \Rightarrow (x_6,y_6)=(x_5+1,y_5-1)=(6,4)$, $p1_6=p1_5+2r_y^2x_6-2r_x^2y_6+r_y^2=244$, $2r_y^2x_6=360+72=432$ a $2r_x^2y_6=640-128=512$.
   • $i=6:$ $p1_6 \gt 0 \Rightarrow (x_7,y_7)=(x_6+1,y_6-1)=(7,3)$, $2r_y^2x_7=432+72=504$ a $2r_x^2y_7=512-128=384$. Platí $2r_y^2x_7 \geq 2r_x^2y_7$, preto prechádzame do druhej oblasti.
4. $(x_0,y_0)=(7,3)$ a teda $p2_0=r_y^{2}(x_0+\frac{1}{2})^{2}+r_x^{2}(y_0-1)^{2}-r_x^{2}r_y^{2}=-23$.
5. • $i=0:$ $p2_0 \lt 0 \Rightarrow (x_1,y_1)=(x_0+1,y_0-1)=(8,2)$, $p2_1=p2_0+2r_y^2x_1-2r_x^2y_1+r_x^2=233$, $2r_y^2x_1=504+72=576$ a $2r_x^2y_1=384-128=256$.
   • $i=1:$ $p2_1 \gt 0 \Rightarrow (x_2,y_2)=(x_1,y_1-1)=(8,1)$, $p2_2=p2_1+2r_x^2y_2+r_x^2=169$, $2r_y^2x_2=576$ a $2r_x^2y_2=256-128=128$.
   • $i=2:$ $p2_2 \gt 0 \Rightarrow (x_3,y_3)=(x_2,y_2-1)=(8,0)$, algoritmus končí, pretože sme sa dostali na hranicu I. oktantu. Výsledné body možno vidieť na Obr. 4.
6. Určíme súmerné body v ostatných oktantoch. Výslednú elipsu možno vidieť na Obr. 4.
7. Posunieme každú hodnotu pixla do stredu $(0,7)$. Teda dostaneme body: $(0,13),(1,13),(2,13),(3,13),(4,12), ...$

Interaktívny applet

Pseudokód

Implementácia Bresenhamovho stredového elipsového algoritmu je zhrnutá v nasledujúcom pseudokóde. Na vstupe sú parametre $r_x$, $r_y$ a stred elipsy$(x_C,y_C)$.

Literatúra

Bresenhamov stredový elipsový algoritmus je podrobne spracovaný v [3] od strany 102. Je uvedený aj v [2] od strany 88, avšak je uvedený iba výsledný vzorec na výpočet bodov pozdĺž elipsy, bez odvodenia.