Riadkový skenovací algoritmus (Scan line Algorithm)

Princíp algoritmu

Scan Line algoritmus rozkladu mnohouholníka patrí do skupiny algoritmov, ktoré používajú princíp skenovacej priamky: ak je možné vyriešiť problém, úlohu z pohľadu jednej vodorovnej alebo zvislej priamky, urobí sa tak. Úlohu takejto priamky hrá často riadok alebo stĺpec pixlov rastra. Okrem zúženia pohľadu je druhou vlastnosťou skenovacích algoritmov využitie informácií z jedného kroku, v nasledujúcom kroku.

V algoritme bude skenovacia priamka vodorovná s celočíselnými súradnicami. Jej rovnica teda bude $y = y_i$, kde $y_i$ nadobúda celočíselné hodnoty od najmenšej po najväčšiu $y$-ovú súradnicu vrcholov mnohouholníka.

Scan Line algoritmus na rozklad mnohouholníka funguje tak, že v každom kroku zistí prieniky skenovacej priamky so stranami mnohouholníka, tieto prieniky usporiada do dvojíc a úseky medzi dvojicami vyfarbí.

Ak urobíme prienik skenovacej priamky so stranami mnohouholníka, chceme získať párny počet bodov. Preto musíme zo zoznamu strán mnohouholníka vylúčiť vodorovné strany (tie sa vykreslia priamo) a ešte musíme skrátiť zdola strany v neextremálnych bodoch (vo vrcholoch, z ktorých idú strany do opačných polrovín vzhľadom na skenovaciu priamku).

Konkrétna realizácia tohto skrátenia bude zrejmá z inicializácie dátovej štruktúry, ktorú algoritmus používa.

Dátové štruktúry pre Scan Line algoritmus

Základným kameňom dátových štruktúr bude záznam o strane mnohouholníka. Tento záznam bude obsahovať tri čísla:

  • maximálnu $y$-ovú súradnicu strany; je to väčšia z $y$-ových súradníc vrcholov strany, toto číslo použijeme pri rozhodovaní, či je nutné zisťovať prienik strany so skenovacou priamkou
  • $x$-ovú súradnicu bodu s minimálnou y-ovou súradnicou ; toto číslo je vlastne x-ová súradnica bodu, v ktorom skenovacia priamka prvýkrát pretne stranu a v priebehu algoritmu je táto hodnota modifikovaná
  • prevrátenú hodnotu smernice priamky, na ktorej strana leží: $\frac{1}{m} = \frac{x_A-x_B}{y_A-y_B}$, kde A,B sú vrcholy strany.

V predchádzajúcej časti sme hovorili o skrátení strany zdola v neextremálnom vrchole. Toto skrátenie zrealizujeme tak, že druhú hodnotu záznamu pre stranu budeme inicializovať nie na $x$-ovú súradnicu vrcholu strany, ktorý má menšiu $y$-ovú súradnicu, ale ak je tento vrchol neextremálny, na jeho $x$-ovú súradnicu zväčšenú o $\frac{1}{m}$. Pri tomto skrátení vychádzame z toho, že ak na priamke so smernicou $m$ leží bod so súradnicami $[x, y]$, tak na nej leží aj bod so súradnicami$[x+\frac{1}{m}, y+1](m(x+\frac{1}{m})+q=mx+q+1=y+1)$.

Algoritmus používa dve dátové štruktúry: tabuľku strán (TS) a tabuľku aktívnych strán (TAS).

TS sa vytvára pri inicializácii a má riadky označené hodnotami, ktoré skenovacia priamka nadobudne v jednotlivých krokoch (celočíselné hodnoty od najmenšej po najväčšiu $y$-ovú súradnicu vrcholov mnohouholníka). V jednotlivých riadkoch je zoznam záznamov strán, ktoré majú túto hodnotu ako svoju minimálnu $y$-ovú súradnicu. Ak je vrchol strany s menšou $y$- ovou súradnicou neextremálny, strana bude zapísaná až v ďalšom riadku TS (pretože je zdola skrátená). Všimnime si, že až teraz, keď je strana zaradená do TS, máme o nej úplnú informáciu.

TAS je zoznam strán, s ktorými má aktuálna skenovacia priamka prienik a vytvára sa počas behu algoritmu vyberaním záznamov o stranách z TS. V tejto tabuľke sa druhá položka záznamu o každej strane mení tak, aby vždy mala hodnotu $x$-ovej súradnice prieniku strany a skenovacej priamky.

Postup výpočtu

Na vstupe algoritmu nech je usporiadaný zoznam vrcholov mnohouholníka s celočíselnými súradnicami. Na výstupe algoritmu musí byť tento mnohouholník rozložený do rastra t.j. v rastri majú byť vyfarbené príslušné obrazové body.

  1. Zisti, ktoré strany mnohouholníka sú vodorovné, ktoré vrcholy neextremálne.
  2. Strany, ktoré nie sú vodorovné zapíš do TS, TAS inicializuj ako prázdnu, teda $y=y_{min}$
  3. Kým TS alebo TAS sú neprázdne opakuj:
    1. Vyber TS strany v riadku y a daj ich do TAS.
    2. Usporiadaj strany v TAS podľa $x$-ovej súradnice (druhá položka v jednotlivých záznamoch).
    3. Vyber za sebou idúce úseky a vykresli ich.
    4. Zruš tie strany v TAS, pre ktoré $y_{max} = y$.
    5. Pre strany v TAS zmeň $x$ na $x+\frac{1}{m}$.
    6. $y=y+1$.

Príklad

Pre mnohouholník $A_{0}A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}$, kde $A_{0}=(0,4)$, $A_{1}=(3,0)$, $A_{2}=(5,3)$, $A_{3}=(4,5)$, $A_{4}=(3,2)$, $A_{5}=(2,7)$, $A_{6}=(1,7)$, opíšeme TS, jednotlivé kroky TAS ako aj výstup algoritmu a jednotlivé vykresľované úseky. Mnohouholník môžeme vidieť na Obr. 1.

Obr. 1 - Príklad mnohouholníka
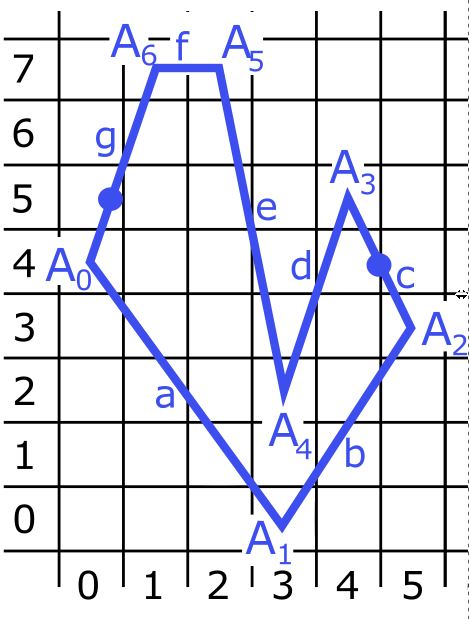
  1. Na obrázku môžeme vidieť, že mnohouholník má jednu vodorovnú hranu $f$, tú do TS nezaradíme. Tiež obsahuje dva neextremálne vrcholy $A_{0}$ a $A_{2}$.
  2. $y_{min}=0$ a $y_{max}=7$ a TS vyzerá nasledovne:
    • $0:$ $a=4\mid 3\mid -\frac{3}{4}$, $b=3\mid 3\mid\frac{2}{3}$
    • $1:$
    • $2:$ $d=5\mid 3\mid \frac{1}{3}$, $e=7\mid 3\mid-\frac{1}{5}$
    • $3:$
    • $4:$ $c=5\mid 5-\frac{1}{2}\mid -\frac{1}{2}$
    • $5:$ $g=7\mid 0+\frac{1}{3}\mid \frac{1}{3}$
    • $6:$
    • $7:$
    • $i=0:$
      1. TAS: $a=4\mid 3\mid -\frac{3}{4}$, $b=3\mid 3\mid\frac{2}{3}$.
      2. TAS sa po usporiadaní nezmení.
      3. Vykresli úsek $[3,0]$ až $[3,0]$, t.j. pixel $[3,0]$.
      4. Z TAS sa žiadna hrana nezruší.
      5. TAS: $a=4\mid \frac{9}{4}\mid -\frac{3}{4}$, $b=3\mid \frac{11}{3}\mid\frac{2}{3}$.
      6. $y=1$.
    • $i=1:$
      1. TAS sa nezmení, t.j. TAS: $a=4\mid 3\mid -\frac{3}{4}$, $b=3\mid 3\mid\frac{2}{3}$.
      2. TAS sa po usporiadaní nezmení.
      3. Vykresli úsek $[\frac{9}{4},1]$ až $[\frac{11}{3},1]$, t.j. pixle $[2,1]$,$[3,1]$,$[4,1]$.
      4. Z TAS sa žiadna hrana nezruší.
      5. TAS: $a=4\mid \frac{6}{4}\mid -\frac{3}{4}$, $b=3\mid \frac{11}{3}\mid\frac{2}{3}$.
      6. $y=2$.
    • $i=2:$
      1. TAS: $a=4\mid \frac{6}{4}\mid -\frac{3}{4}$, $b=3\mid \frac{11}{3}\mid\frac{2}{3}$, $d=5\mid 3\mid \frac{1}{3}$, $e=7\mid 3\mid -\frac{1}{3}$.
      2. TAS: $a=4\mid \frac{6}{4}\mid -\frac{3}{4}$, $d=5\mid 3\mid \frac{1}{3}$, $e=7\mid 3\mid -\frac{1}{3}$, $b=3\mid \frac{11}{3}\mid\frac{2}{3}$.
      3. Vykreslia sa úseky $[\frac{6}{4},2]$ až $[3,2]$ a $[3,2]$ až $[\frac{13}{3},2]$, t.j. pixle $[2,2]$,$[3,2]$,$[4,2]$.
      4. Z TAS sa žiadna hrana nezruší.
      5. TAS: $a=4\mid \frac{3}{4}\mid -\frac{3}{4}$, $d=5\mid \frac{10}{3}\mid \frac{1}{3}$, $e=7\mid \frac{14}{5}\mid -\frac{1}{5}$, $b=3\mid 5\mid\frac{2}{3}$.
      6. $y=3$.
    • $i=3:$
      1. TAS sa nemení.
      2. TAS: $a=4\mid \frac{3}{4}\mid -\frac{3}{4}$, $e=7\mid \frac{14}{5}\mid -\frac{1}{5}$, $d=5\mid \frac{10}{3}\mid \frac{1}{3}$, $b=3\mid 5\mid\frac{2}{3}$.
      3. Vykreslia sa úseky $[\frac{3}{4},3]$ až $[\frac{14}{3},3]$ a $[\frac{10}{3},3]$ až $[5,3]$, t.j. pixle $[1,3]$,$[2,3]$, $[3,3]$, $[4,3]$, $[5,3]$.
      4. TAS: $a=4\mid \frac{3}{4}\mid -\frac{3}{4}$, $e=7\mid \frac{14}{5}\mid -\frac{1}{5}$, $d=5\mid \frac{10}{3}\mid \frac{1}{3}$.
      5. TAS: $a=4\mid 0\mid -\frac{3}{4}$, $e=7\mid \frac{13}{5}\mid -\frac{1}{5}$, $d=5\mid \frac{11}{3}\mid \frac{1}{3}$.
      6. $y=4$.
    • $i=4:$
      1. TAS sa nemení.
      2. TAS: $a=4\mid 0\mid -\frac{3}{4}$, $e=7\mid \frac{13}{5}\mid -\frac{1}{5}$, $d=5\mid \frac{11}{3}\mid \frac{1}{3}$, $c=5\mid \frac{9}{2}\mid -\frac{1}{2}$.
      3. TAS sa po usporiadaní nezmení.
      4. Vykreslia sa úseky $[0,4]$ až $[\frac{13}{5},4]$ a $[\frac{11}{3},4]$ až $[\frac{9}{2},4]$, t.j. pixle $[0,4]$,$[1,4]$, $[2,4]$, $[3,4]$, $[4,4]$, $[5,4]$.
      5. TAS: $e=7\mid \frac{13}{5}\mid -\frac{1}{5}$, $d=5\mid \frac{11}{3}\mid \frac{1}{3}$, $c=5\mid \frac{9}{2}\mid -\frac{1}{2}$.
      6. TAS: $e=7\mid \frac{12}{5}\mid -\frac{1}{5}$, $d=5\mid 4\mid \frac{1}{3}$, $c=5\mid 4\mid -\frac{1}{2}$.
      7. $y=5$.
    • $i=5:$
      1. TAS sa nemení.
      2. TAS: $e=7\mid \frac{12}{5}\mid -\frac{1}{5}$, $d=5\mid 4\mid \frac{1}{3}$, $c=5\mid 4\mid -\frac{1}{2}$, $g=7\mid \frac{1}{3}\mid \frac{1}{3}$.
      3. TAS: $g=7\mid \frac{1}{3}\mid \frac{1}{3}$, $e=7\mid \frac{12}{5}\mid -\frac{1}{5}$, $d=5\mid 4\mid \frac{1}{3}$, $c=5\mid 4\mid -\frac{1}{2}$.
      4. Vykreslia sa úseky $[\frac{1}{3},5]$ až $[\frac{12}{5},5]$ a $[4,5]$ až $[4,5]$, t.j. pixle $[0,5]$,$[1,5]$, $[2,5]$, $[4,5]$.
      5. TAS: $g=7\mid \frac{1}{3}\mid \frac{1}{3}$, $e=7\mid \frac{12}{5}\mid -\frac{1}{5}$.
      6. TAS: $g=7\mid \frac{2}{3}\mid \frac{1}{3}$, $e=7\mid \frac{11}{5}\mid -\frac{1}{5}$.
      7. $y=6$.
    • $i=6:$
      1. TAS sa po usporiadaní nezmení.
      2. Vykreslí sa úsek $[\frac{2}{3},6]$ až $[\frac{11}{5},6]$, t.j. pixle $[1,6]$, $[2,6]$.
      3. Z TAS sa žiadna hrana nezruší.
      4. TAS: $g=7\mid 1\mid \frac{1}{3}$, $e=7\mid 2\mid -\frac{1}{5}$.
      5. $y=7$.
    • $i=7:$
      1. TAS sa nemení.
      2. TAS sa po usporiadaní nezmení.
      3. Vykreslí sa úsek $[1,7]$ až $[2,7]$, t.j. pixle $[1,7]$, $[2,7]$.
      4. TAS = $\emptyset$.
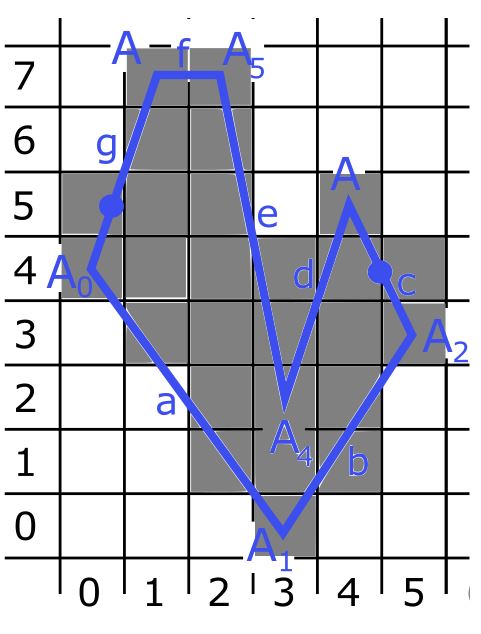
      5. $y=y_{max}$, algoritmus končí. Výsledok je zobrazený na Obr. 2.
Obr. 2 - Výsledný vyplnený mnohouholník

Ďalšie riešené a neriešené príklady.

Pseudokód

Pseudokód Scan-line algoritmu môžeme nájsť na strane 122 v literatúre [3]. Pre jeho veľký rozsah ho tu neuvádzame.

Literatúra

Algoritmus Scan-line vieme nájsť podrobne spracovaný v [3] na strane 117 ako aj v slovenskej literatúre [1] na strane 70 a [2]. Je v krátkosti spomenutý aj v kapitole o rasterizovaní polygónov v [7].