Bresenhamov stredový algoritmus rasterizácie úsečky (Bresenham's Midpoint Line Algorithm)

Princíp algoritmu

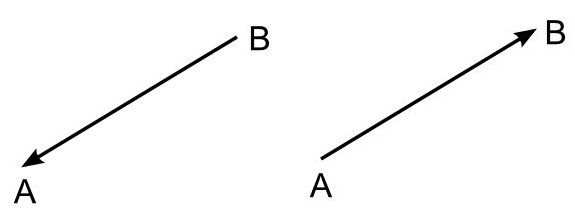
Orientovaná úsečka je nenulová úsečka, ktorej krajné body sú usporiadané. Hovoríme o začiatočnom a koncovom bode orientovanej úsečky (Obr. 1). Hovoríme tiež, že orientovaná úsečka zo svojho začiatočného bodu vychádza a do koncového bodu vchádza. Orientovaná úsečka orientuje prirodzeným spôsobom priamku, na ktorej leží a naopak. Orientáciu úsečky môžeme intuitívne vnímať ako jeden z dvoch smerov pohybu po nej [8].

Obr. 1 - Orientovaná úsečka $BA$ a orientovaná úsečka $AB$

Uvažujeme orientovanú úsečku $AB$, kde $x_A \lt x_B$ (bod $A$ je vľavo od bodu $B$) a smernica $m$ úsečky $AB$ je $0 \leq m \leq 1$ (Obr. 2.).

Obr. 2 - Úsečka $AB$

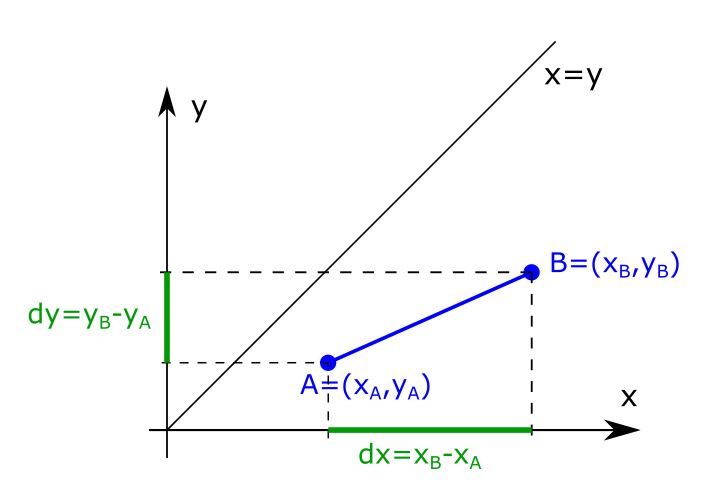
Rovnicu priamky potom možno napísať v implicitnom tvare $f(x,y)=ax+by+c=0$, kde $a=dy, b=-dx, c=dx.y_B-dy.x_B$. Všimnime si, že všetky koeficienty sú celočíselné. Budeme používať ekvivalentnú reprezentáciu priamky $f(x,y)=2ax+2by+2c=0$. Kvôli vhodne zvolenej reprezentácii sa presunieme do celočíselnej aritmetiky.

Táto priamka rozdeľuje rovinu $E^{2}$ na dve polroviny (Obr. 3):

  • $E^{2}_{-}=\lbrace (x,y); f(x,y) \lt 0 \rbrace$. Je to otvorená polrovina, ktorú nazývame ľavá polrovina.
  • $E^{2}_{+}=\lbrace (x,y); f(x,y)\geq 0 \rbrace$. Je uzavretá polrovina a nazývame ju pravá polrovina.
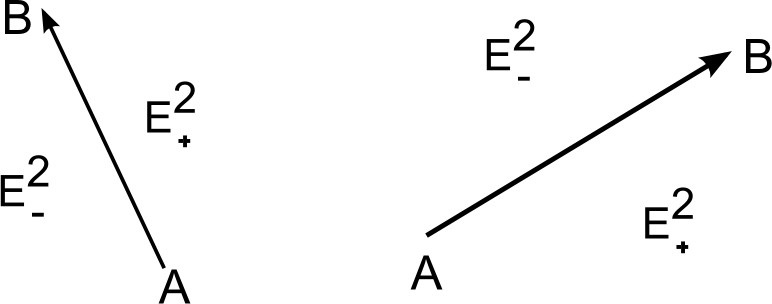
Obr. 3 - Polroviny vzhľadom na orientovanú úsečku $AB$

Z toho môžeme povedať, že:

  • bod $X=(x,y)$ leží vpravo od priamky $AB \Leftrightarrow f(x,y) \gt 0$
  • bod $X=(x,y)$ leží vľavo od priamky $AB \Leftrightarrow f(x,y) \lt 0$
  • bod $X=(x,y)$ leží na priamke $AB \Leftrightarrow f(x,y)=0$.

Predpoklad, že pre smernicu vykresľovanej úsečky platí $0 \leq m \leq 1$, môžeme odstrániť. Ak $|m| \gt 1$, tak zámena $x \leftrightarrow y$ vedie k úsečke s prevrátenou hodnotou smernice. Ak $m \lt 0$, algoritmus vieme modifikovať zámenou prírastok $\leftrightarrow$ úbytok alebo stúpanie $\leftrightarrow$ klesanie. Výmenou vstupných bodov $A\leftrightarrow B$ je možné vždy zabezpečiť kreslenie zľava doprava.

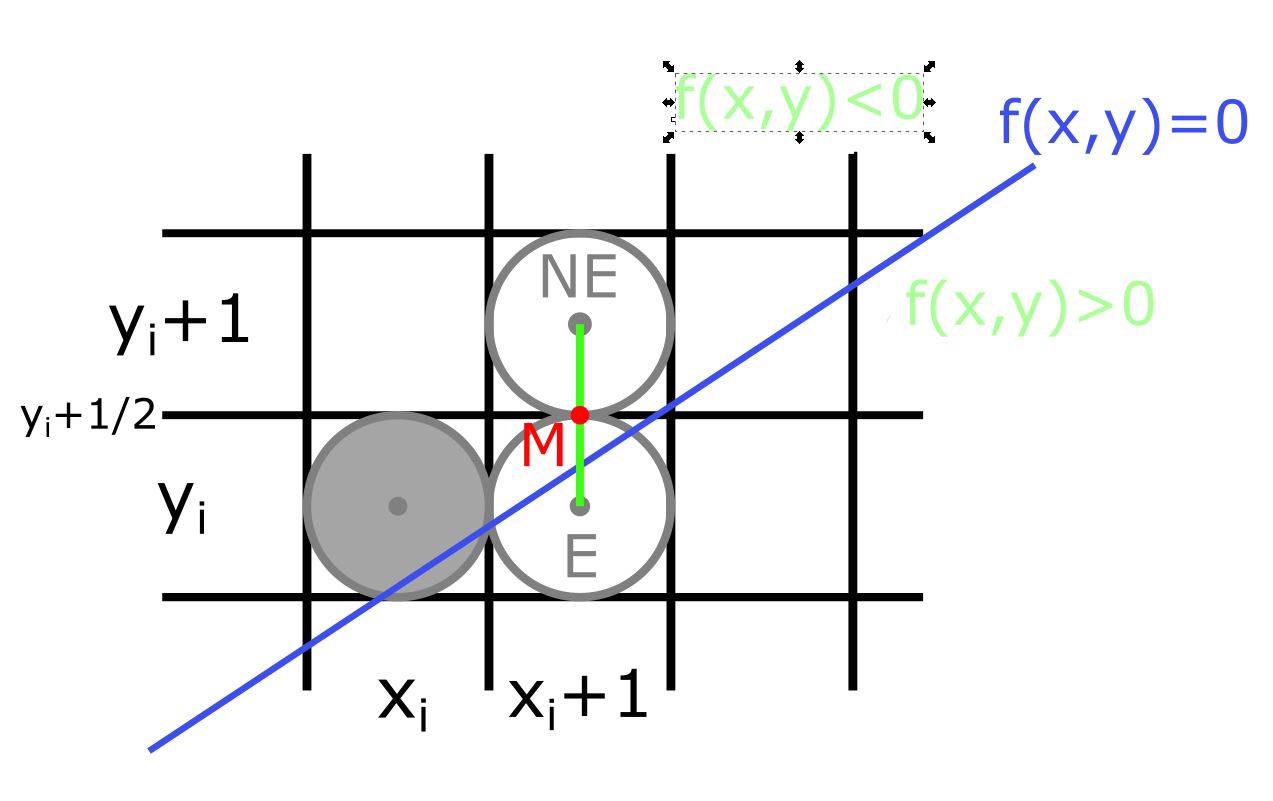
Opäť uvažujme, že pre smernicu platí $0 \lt m \lt 1$. Pri rasterizácii sme dosiahli pixel $(x_i,y_i)$. Potrebujeme rozhodnúť, ktorý z nasledujúcich pixlov $E=(x_i +1,y_i)$ alebo $NE=(x_i+1,y_i+1)$ vykreslíme.

Použijeme bod $M=stred(E, NE)=(x_i+1,y_i+\frac{1}{2})$ a jeho polohu vzhľadom na priamku $f(x,y)$ (Obr. 4). Označíme $D=f(M)=2a(x_i+1)+2b(y_i+\frac{1}{2})+2c$=$ 2ax_i+2by_i+(2a+b+2c) \in \mathbb{N}$. Zrejme platí:

  • Ak $D \gt 0$, tak bod $M$ leží v $E^{2}_{+}$ a z uvažovaných pixlov je bližšie $NE$, ktorý sa vysvieti.
  • Ak $D \lt 0$, tak bod $M$ leží v $E^{2}_{-}$ a bližšie je bod $E$, ten sa rozsvieti.
  • Ak nastáva $D=0$ vysvietime hociktorý z bodov $NE,E$, zvyčajne $NE$.
Obr. 4 - Výber NE resp. E

Je výhodné, že $D$ je celočíselné, ale jeho výpočet si vyžaduje dve násobenia a dve sčítania, ak nemeniaca sa zložka v zátvorke je prepočítaná. Jedným z veľmi šikovných trikov je však, že hodnota $D$ sa počíta prírastkovo.

Predpokladajme, že poznáme aktuálnu hodnotu $D$ a chceme vypočítať jeho nasledujúcu hodnotu:

  • Ak sme ako nový vysvietený pixel vybrali $E=(x_i+1,y_i)$, tak v nasledujúcom kroku k nemu prislúcha nový stred $M_{new}=((x_i+1)+1,y_i+\frac{1}{2})$ a nové $D_{new}=f(M_{new})=2a(x_i+2)+2b(y_i+\frac{1}{2})+2c$= $2a(x_i+1)+2by_i+(2a+b+2c)=D+2a=D+2dy$
  • Ak sme však ako nový vysvietený pixel vybrali bod $NE=(x_i+1,y_i+1)$, tak k nemu prislúcha nový stred $M_{new}=((x_i+1)+1,(y_i+1)+\frac{1}{2})$ a $D_{new}=f(M_{new})=2a(x_i+2)+2b(y_i+1+\frac{1}{2})+2c$= $2a(x_i+1)+2b(y_i+1)+(2a+b+2c)=D+2a+2b=D+2(dy-dx)$.

Platí teda:

  • Ak $D \lt 0$, tak $D_{new}=D+2dy$ a vysvietime bod $E$
  • Ak $D \geq 0$, tak $D_{new}=D+2(dy-dx)$ a vysvietime bod $NE$

Z toho vyplýva, že parameter $D$ je ekvivalentný parametru $p$ z predchádzajúceho algoritmu a možno ho považovať za rozhodovací parameter Bresenhamovho algoritmu rasterizácie úsečky. Teda algoritmus možno dokončiť ako Bresenhamov line algoritmus.

V literatúre parameter $D$ autori často uprednostňujú pred parametrom $p$ z predchádzajúceho algoritmu, lebo princíp jeho konštrukcie je možno použiť aj v ďalších algoritmoch ako napr. v Bresenhamovom algoritme rasterizácie kružnice.

Postup výpočtu pre $|m| \lt 1$

Kroky algoritmu vieme zhrnúť rovnakým spôsobom ako v predošlom algoritmu, keďže parameter $D$ je ekvivalentný parametru $p$.

  1. Vlož dva krajné body $(x_A, y_A)$ a $(x_B, y_B)$ a zober ľavý (s menšou $x$-ovou súradnicou) ako bod $(x_0, y_0)$.
  2. Nahraj $(x_0, y_0)$ do frame buffera, teda zobraz bod $(x_0, y_0)$ do rastra.
  3. Vypočítaj konštanty $dx$, $dy$, $2dy$, $2(dy - dx)$ a urči počiatočnú hodnotu parametra $D=f(M)=2ax_i+2by_i+(2a+b+2c)$, kde $M=(x_i+1,y_i+\frac{1}{2})$.
  4. V každej pozícií $x_i$ začínajúc s $i=0$ pozdĺž úsečky vykonaj test:
    1. Ak $D \lt 0$: nasledujúci bod je $(x_{i+1}, y_{i+1})=(x_i+1,y_i)$ a $D_{new}=D+2 dy$.
    2. Inak je nasledujúci bod $(x_{i+1}, y_{i+1})=(x_i+1,y_i+1)$ a $D_{new}=D+2 dy-2 dx$
    3. Vykresli bod $(x_{i+1}, y_{i+1})$ a $D=D_{new}$.
  5. Opakuj krok 4. $dx$-krát.

Príklad

Ako sme uviedli parameter $D$ je ekvivalentný parametru $p$ z Bressenhamovho algoritmu rasterizácie úsečky, postup výpočtu príkladu je rovnaký ako v predchádzajúcom príklade. To isté platí aj pre implementáciu Bresenhamovho stredového algoritmu pre smernicu úsečky $0 \lt m \lt 1$.

Ďalšie riešené a neriešené príklady.

Literatúra

Bresenhamov stredový algoritmus sa nenachádza v [3] ani v [7]. Zo slovenskej/českej literatúry sa taktiež nenachádza v [1] ani [2].