Počítačová grafika

Algoritmus Cyrus-Beck

Princíp algoritmu

Staršia verzia Liang-Barského algoritmu je známa ako algoritmus Cyrus-Beck. Je to rýchlejšia metóda ako Algoritmus Cohen-Sutherland. Je to orezávanie do konkrétneho okna, no nie nutne axiálneho.

Je založený na hľadaní tzv. vstupného bodu úsečky $AB$ do okna, ktorý je určený maximálnym vstupným parametrom $t_{e}$ a výstupného bodu úsečky $AB$ z okna, ktorý je určený zasa minimálnym výstupným parametrom $t_{o}$ v intervale $\lt0,1\gt$. Predpokladá sa, že úsečka $AB$ je určená parametrickým vyjadrením: \begin{equation} P(t) = A + dt, \end{equation} kde vektor $s = B - A$ a $t \in \lt0,1\gt$ a chceme určiť jej prienik so stranou E (edge) konvexného mnohouholníka určenou bodom P a vonkajším normálovým vektorom $\textbf{n}$.

Vo všeobecnosti pre uhol vektora a vonkajší normálový vektor strany mnohouholníka platí:

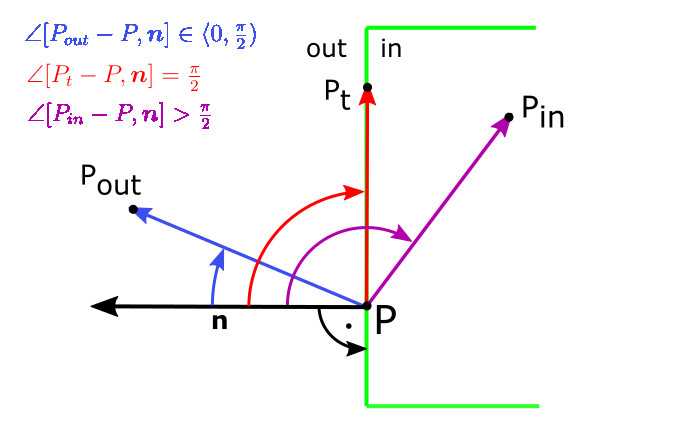
• $\angle [P_{out}-P,\textbf{n}]\in \langle 0,\frac{\pi}{2})$
• $\angle [P_{in}-P,\textbf{n}] \gt \frac{\pi}{2}$
• $\angle [P_t-P,\textbf{n}]= \frac{\pi}{2}$

a pre uhol vektora a vnútorný normálový vektor strany mnohouholníka platí:

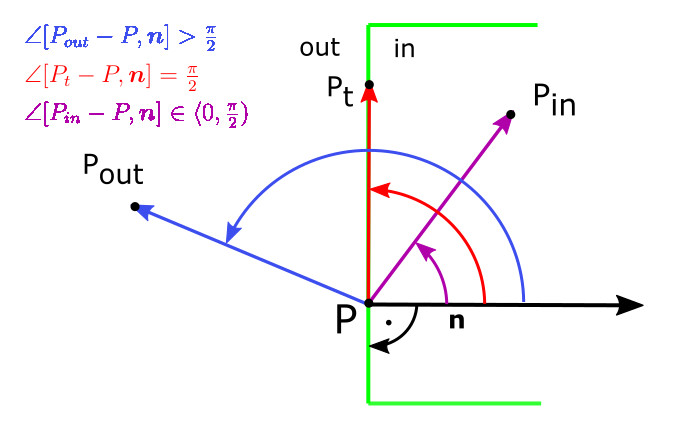
• $\angle [P_{out}-P,\textbf{n}] \gt \frac{\pi}{2}$
• $\angle [P_{in}-P,\textbf{n}]\in \langle 0,\frac{\pi}{2})$
• $\angle [P_t-P,\textbf{n}] = \frac{\pi}{2}$

Platí:

• $P(t)$ je vonkajším bodom, ak $\angle [P(t) - P,\boldsymbol{n}]\in \langle 0,\frac{\pi}{2})\Leftrightarrow [P(t) - P].\boldsymbol{n} \gt 0$
• $P(t)$ je vnútorným bodom, ak $\angle [P(t) - P,\boldsymbol{n}]> \frac{\pi}{2}\Leftrightarrow [P(t) - P].\boldsymbol{n} \lt 0$
• $P(t)$ leží na strane $E$, ak $\angle [P(t) - P,\boldsymbol{n}]= \frac{\pi}{2}$ $\Leftrightarrow$ $ [P(t) - P].\boldsymbol{n} = 0 \Leftrightarrow (A - P+t.\boldsymbol{d}).\boldsymbol{n} = 0 \Leftrightarrow (A - P).\boldsymbol{n}+t.\boldsymbol{(d.n)} = 0 $ $\Leftrightarrow$ $ \Big[\boldsymbol{(d.n)}\neq 0 \land t=-\frac{(A-P).\boldsymbol{n}}{\boldsymbol{(d.n)}}\Big]\lor \Big[\boldsymbol{(d.n)}= 0 \land (A-P).\boldsymbol{n}=0\Big] \lor \Big[\boldsymbol{(d.n)}= 0 \land (A-P).\boldsymbol{n}\neq 0\Big]$. Teda $t=-\frac{(A-P).\boldsymbol{n}}{\boldsymbol{(d.n)}}$, kde $\boldsymbol{(d.n)}\neq 0$.

Pokiaľ priamka $AB$ obsahuje stranu mnohouholníka t.j. prienikom priamky a mnohouholníka je táto strana, čiže strana je orezaním priamky $AB$ mnohouholníkom – algoritmus končí.

Ak priamka $AB$ a strana $E$ nemajú spoločný ani jeden bod, čiže priamka je so stranou $E$ rovnobežná, pričom môže, ale nemusí pretínať ďalšie strany – prejdeme k ďalšej strane.

Môžu nastať dve situácie:

• Ak $\boldsymbol{d.n} \lt 0 $, nazveme ho potenciálne vstupným parametrom a označíme $t_e$. Bod $P(t_e)$ budeme nazývať potenciálne vstupným bodom úsečky $AB$ do okna.
• Ak $\boldsymbol{d.n} \gt 0$, nazveme ho potenciálne výstupným parametrom a označíme $t_o$. Bod $P(t_o)$ budeme nazývať potenciálne výstupným bodom úsečky $AB$ z okna.

Nevýhodou tohto algoritmu je, že nevieme ošetriť prípad, keď sa úsečka nachádza celá mimo mnohouholníka.

Postup výpočtu

Na ilustráciu algoritmu Cyrus-Beck si ukážeme orezanie úsečky s krajnými bodmi $A = (x_A, y_A)$ a $B = (x_B, y_B)$ do mnohouholníka určeného vrcholmi $A_i$.

1. Zvolíme si jednu z dvoch orientácií mnohouholníka, nech je kladná, t.j. proti smeru hodinových ručičiek. Uvažujeme vnútorné normály strán mnohouholníka.
2. Inicializácia $t_e=0, t_o=1$, urči smerový vektor orezávanej úsečky $\boldsymbol{s}=B-A$.
3. Pre každý vektor hrany $\boldsymbol{e_i}$ a jemu prislúchajúci normálový vektor $\boldsymbol{n_i}$ vykonáme:
   1. Urči vektor $\boldsymbol{e_i}$ a normálový vektor danej hrany $\boldsymbol{n_i}$ a jeden bod ležiaci na hrane, nech je to bod $A_i$
   2. Urči skalárny súčin $u = \langle \boldsymbol{s}, \boldsymbol{n_i}\rangle$
   3. Urči $t = \frac{\langle P_i-A, \boldsymbol{n_i}\rangle}{u}$
   4. Ak $u \lt 0$ platí $t_o=min(t_o,t)$. Ak $u \gt 0$ platí $t_e=max(t_e,t)$.
4. Výsledná orezaná úsečka má krajné body:
   • Pre $t_e$: $P(t_e)= A+ t_e(B-A)$
   • Pre $t_o$: $P(t_o)= A+ t_o(B-A)$

Príklad

Na ilustráciu algoritmu Cyrus-Beck si ukážeme orezanie úsečky s krajnými bodmi $A = (x_A, y_A)=(-2,2)$ a $B = (x_B, y_B)=(8,3)$ do mnohouholníka určeného vrcholmi $A_i$, kde $A_1=(2,1)$, $A_2=(5,2)$, $A_3=(4,5)$ a $A_4=(2,3)$.

1. Zvolíme si jednu z dvoch orientácií mnohouholníka, nech je kladná, t.j. proti smeru hodinových ručičiek. Uvažujeme vnútorné normály strán mnohouholníka.
2. $t_e=0, t_o=1$ a $\boldsymbol{s}=(8,3)-(-2,2)=(10,1)$.
3. • $i=1:$
     1. $\boldsymbol{e_1}=A_2-A_1=(5,2)-(2,1)=(3,1)$, $\boldsymbol{n_1}=(-1,3)$, $P_1=(3,1)$.
     2. $u = \langle \boldsymbol{s}, \boldsymbol{n_1}\rangle= \langle (10,1), (-1,3)\rangle=-7$
     3. $t = \frac{\langle P_1-A, \boldsymbol{n_1}\rangle}{u} = \frac{\langle (5,-1), (-1,3)\rangle}{-7}=\frac{8}{7}$
     4. $u \lt 0$, teda $t_o=min(1,\frac{8}{7})=1$.
   • $i=2:$
     1. $\boldsymbol{e_2}=A_3-A_2=(4,5)-(5,2)=(-1,3)$, $\boldsymbol{n_2}=(-3,-1)$, $P_2=(5,2)$.
     2. $u = \langle \boldsymbol{s}, \boldsymbol{n_2}\rangle= \langle (10,1), (-3,-1)\rangle=-31$
     3. $t = \frac{\langle P_2-A, \boldsymbol{n_2}\rangle}{u} = \frac{\langle (7,0), (-3,-1)\rangle}{-31}=\frac{21}{31}$
     4. $u \lt 0$, teda $t_o=min(1,\frac{21}{31})=\frac{21}{31}$.
   • $i=3:$
     1. $\boldsymbol{e_3}=A_4-A_3=(2,3)-(4,5)=(-2,2)$, $\boldsymbol{n_3}=(2,-2)$, $P_3=(4,5)$.
     2. $u = \langle \boldsymbol{s}, \boldsymbol{n_3}\rangle= \langle (10,1), (2,-2)\rangle=18$
     3. $t = \frac{\langle P_3-A, \boldsymbol{n_3}\rangle}{u} = \frac{\langle (6,3), (-3,-1)\rangle}{18}=\frac{1}{3}$
     4. $u \lt 0$, teda $t_o=min(\frac{21}{31}, \frac{1}{3})=\frac{21}{31}$.
   • $i=4:$
     1. $\boldsymbol{e_4}=A_1-A_4=(2,1)-(2,3)=(0,-2)$, $\boldsymbol{n_4}=(2,0)$, $P_4=(2,3)$.
     2. $u = \langle \boldsymbol{s}, \boldsymbol{n_4}\rangle= \langle (10,1), (2,0)\rangle=20$
     3. $t = \frac{\langle P_4-A, \boldsymbol{n_4}\rangle}{u} = \frac{\langle (4,1), (2,0)\rangle}{20}=\frac{2}{5}$
     4. $u \gt 0$, teda $t_e=max(0, \frac{2}{5})=\frac{2}{5}$.
4. Krajné body orezanej úsečky:
   • Pre $t_e$: $P(t_e)= (-2,2)+ \frac{21}{31}(10,1)=(\frac{148}{31},\frac{83}{31})$
   • Pre $t_o$: $P(t_o)= (-2,2)+ \frac{2}{5}(10,1)=(2,\frac{12}{5})$
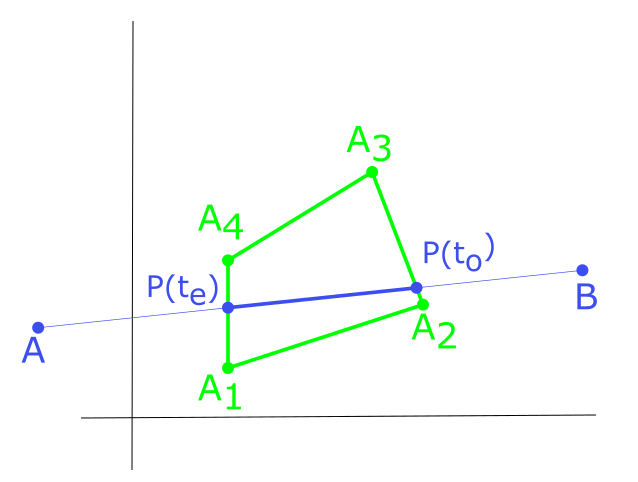
5. Výslednú orezanú úsečku môžete vidieť na Obr. 3.

Ďalšie riešené a neriešené príklady.

Pseudokód

Implementácia algoritmu Cyrus-Beck je zhrnutá v nasledujúcom pseudokóde. Na vstupe sú dva krajné body úsečky $A$ a $B$.

Funkcia ROUND(x) predstavuje zaokrúhlenie hodnoty $x$ na celé čísla.

Literatúra

Môžeme sa s ním stretnúť v [1] od strany 28 pod názvom parametrické orezávanie a v českej literatúre [2] môžeme nájsť vysvetlenie tohto algorimtmu od strany 107. V anglickej literatúre [3] sa tento algoritmus neuvádza.