Algoritmy na rasterizáciu elipsy
Elipsa $E$ je definovaná ako množina všetkých bodov roviny, ktoré majú od dvoch rôznych pevných bodov $F_1$, $F_2$ rovnaký súčet vzdialeností, ktorý je väčší ako vzdialenosť týchto bodov (Obr. 1).
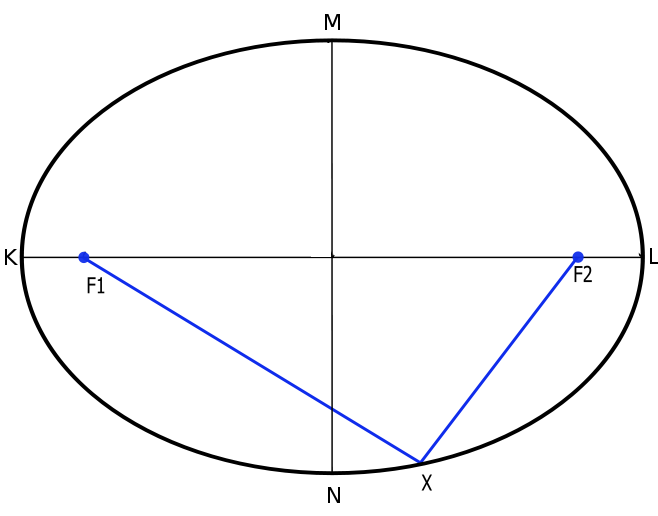
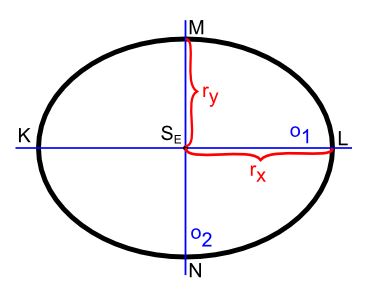
Body $F_1$ a $F_2$ nazývame ohniská elipsy. Priamka prechádzajúca týmito dvoma bodmi sa nazýva hlavná os elipsy a označíme ju $o_1$. Stred úsečky $F_1F_2$ nazývame stred elipsy a označíme ho ako $S_E=(x_C,y_C)$. Priamku kolmú na os $o_1$ prechádzajúcu bodom $S_E$ nazývame vedľajšia os elipsy a označíme ju $o_2$. Body, v ktorých elipsa $E$ pretne os $o_1$, nazývame hlavné vrcholy (body $K$ a $L$ na Obr. 2) a body prieniku osi $o_2$ s elipsou $E$ nazývame vedľajšie vrcholy elipsy (body $M$,$N$ na Obr. 2).
Dĺžku úsečky $S_E L$ označíme ako $r_x$ a nazývame ju hlavná poloos elipsy. Analogicky dĺžku úsečky $S_E M$ označujeme $r_y$ a nazývame vedľajšia poloos.
Ďalej sa budeme zaoberať iba špeciálnou polohou elipsy, v ktorej je hlavná a vedľajšia os rovnobežná so súradnicovými osami. Túto polohu nazývame základná pozícia elipsy (Obr. 3).
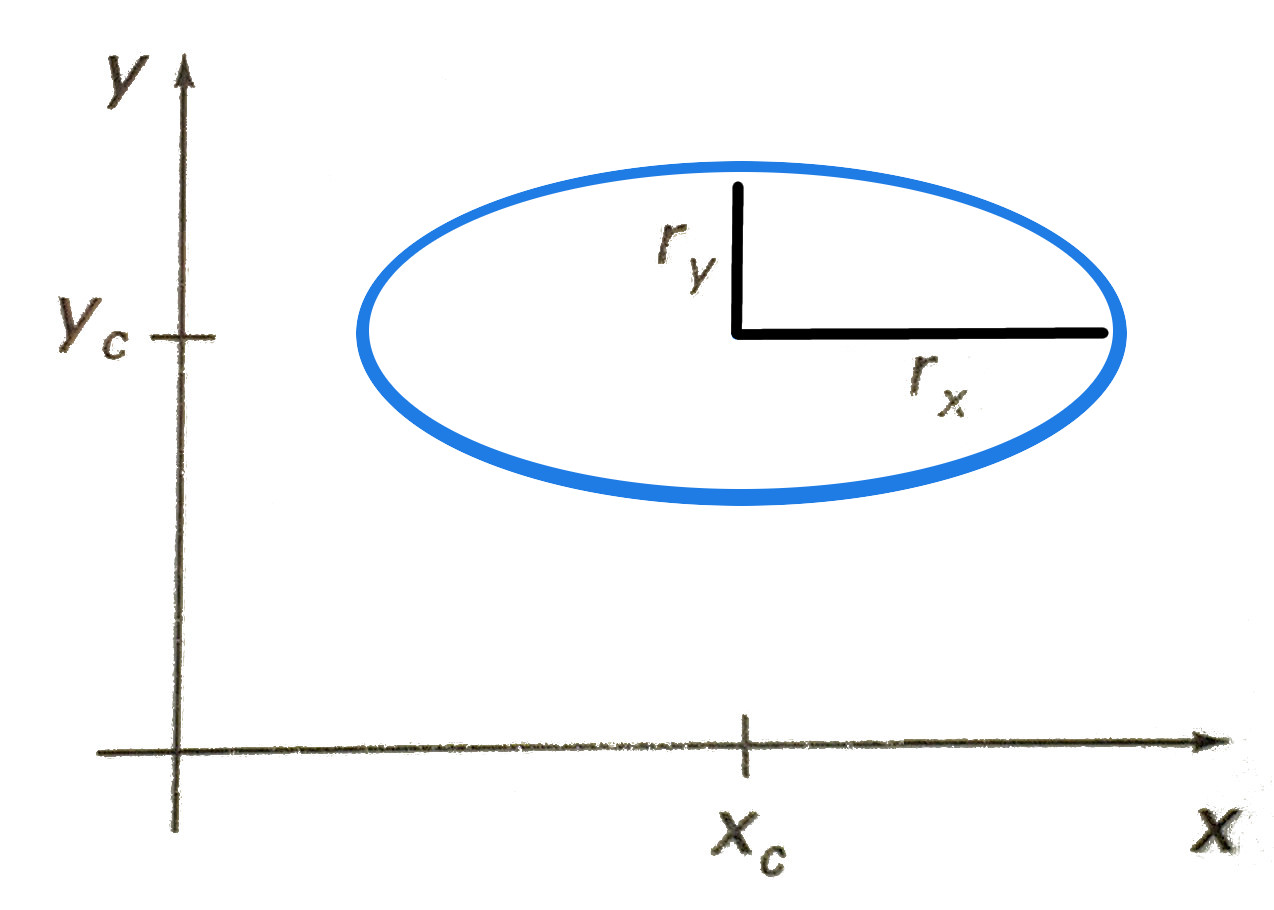
V tomto prípade môžeme rovnicu elipsy zapísať ako \begin{equation} \left( \frac{x-x_C}{r_x}\right)^2+\left( \frac{y-y_C}{r_y}\right)^2=1 \end{equation}
Pomocou parametrických súradníc vieme elipsu v základnej pozícií vyjadriť pomocou rovníc \begin{equation} \begin{split} x(t)=x_C+r_x \cos(t), \\ y(t)=y_C+r_y \sin(t), \end{split} \end{equation} kde parameter $t \in \left\langle 0,2 \pi\right)$.
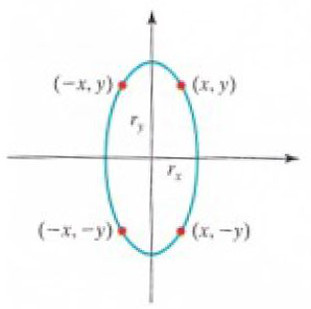
Na zrýchlenie výpočtov pixlov pozdĺž elipsy môžeme využiť súmernosti elipsy. Elipsa v základnej pozícii na rozdiel od kružnice je súmerná iba podľa súradnicových osí $x$ a $y$. Preto môžeme vyčísliť pozície pixelov v jednom kvadrante a ostatné dostaneme zo súmerností (Obr. 4).
V nasledujúcej podkapitole si ukážeme jeden algoritmus na zobrazenie elipsy do rastra, Bresenhamov stredový elipsový algoritmus. Na vstupe algoritmu máme polomer stred $(x_C,y_C)$ elispy $E$ a hodnoty $r_x$ a $r_y$. Na výstupe dostaneme množinu bodov rastra, ktoré aproximujú danú elipsu $E$.