Algoritmy na rasterizáciu úsečky
Úsečka je vo všeobecnosti vyjadrená neceločíselnými súradnicami koncových bodov. Algoritmy na vykresľovanie do rastra ale počítajú s celočíselnými súradnicami. Preto sa na vstupe algoritmu koncové body zaokrúhľujú do celočíselnej aritmetiky. Chyba, ku ktorej v dôsledku zaokrúhlenia dôjde, je považovaná za bezvýznamnú (Obr. 1).
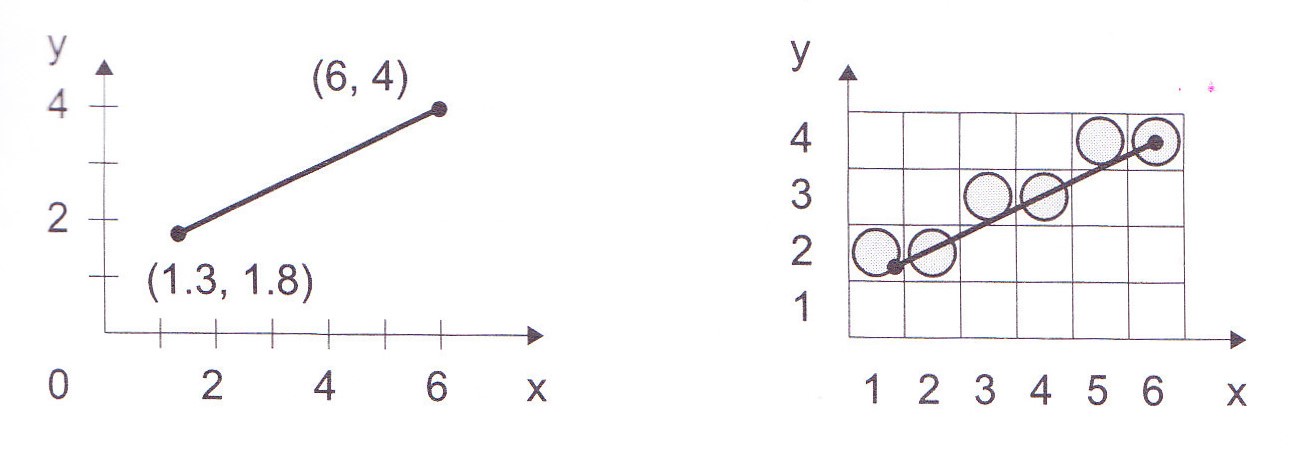
Úsečka je segment priamky a uvedieme tri spôsoby opisu:
- Smernicová rovnica priamky: \begin{equation} y=mx+b, \end{equation} kde $m$ je smernica priamky a $b$ je $y$-ová súradnica priesečníka priamky s osou $y$. Smernica priamky vyjadruje tangens uhla, ktorý zviera priamka s kladnou časťou osi $x$. \\Ak priamka prechádza bodom $O$ (začiatok súradnicovej sústavy), tak $b=0$, t.j.: \begin{equation} y=mx \end{equation}
- Priamka určená dvoma bodmi: Máme dva krajné body úsečky $AB$, $A=(x_A, y_A)$, $B=(x_B, y_B)$, $x_A \neq x_B$, $x_i, y_i \in \mathbb{N} \cup \lbrace0\rbrace, x_i\in\langle x_A,x_B\rangle, y_i\in\langle y_A,y_B\rangle$. Priamku určenú týmito dvoma bodmi dostaneme zo smernicového tvaru rovnice: \begin{equation} y-y_A=\frac{y_B-y_A}{x_B-x_A}(x-x_A) \end{equation} Po úprave $y=mx+b$, kde $m=\frac{y_B-y_A}{x_B-x_A}$ a $b=y_B-mx_A$. Hodnoty $x_B-x_A$ a $y_B-y_A$ vyjadrujú prírastok v smere osi $x$ a $y$ a môžeme ich označiť ako $dx=x_B-x_A$ a $dy=y_B-y_A$. V literatúre sa $dx$ označuje aj ako $\Delta x$ a $dy$ ako $\Delta y$.
- Všeobecná rovnica priamky: Smernicovú rovnicu priamky vieme upraviť na tvar \begin{equation} ax+by+c=0, \end{equation} kde $a,b,c \in \mathbb{R}$. Toto vyjadrenie nazývame všeobecná rovnica priamky.
Ďalej nás budú zaujímať priamky $y=x$ a $y=-x$. Tie rozdelia rovinu na dve oblasti $E_{x}$ a $E_{y}$, z ktorých každá je zjednotením dvoch protiľahlých vrcholových uhlov (Obr. 2).
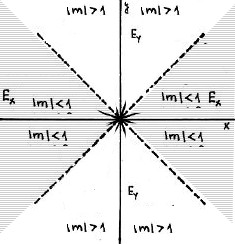
- Oblasť $E_{x}$ obsahuje os $x$-ovú. Je zrejmé, že do oblasti $E_{x}$ patria tie a len tie priamky, ktorých smernice spĺňajú podmienku $|m|\leq 1$ a teda $\mid dy\mid\leq\mid dx \mid$. Sú to priamky s miernym stúpaním resp. klesaním vzhľadom k osi $x$. Ak úsečka patrí do oblasti $E_x$ hovoríme, že má dominantný smer $x$.
- Oblasť $E_{y}$ obsahuje os $y$. Do oblasti $E_{y}$ patria tie a len tie priamky, ktorých smernice spĺňajú podmienku $|m|\geq 1$ a zároveň $\mid dy\mid\geq \mid dx\mid$. To sú priamky so strmým stúpaním resp. klesaním vzhľadom na os $x$, čiže s miernym stúpaním resp. klesaním vzhľadom na os $y$. Ak úsečka patrí do oblasti $E_y$ má dominantný smer $y$.
Hraničné priamky $y=x$ a $y=-x$ môžeme zaradiť do ktorejkoľvek z týchto oblastí, dohodnime sa, že ich zaradíme napr. do oblasti $E_{x}$.
Súradnicové osi $x$ a $y$ rozdelia rovinu na štyri kvadranty (Obr. 3). Ak k nim pridáme ešte priamky $y=x$ a $y=-x$, dostaneme rozdelenie roviny na osem oktantov (Obr. 3). Úsečke $AB$ vieme následne podľa hodnoty smernice $m$ priradiť príslušnosť do kvadrantu alebo oktantu.
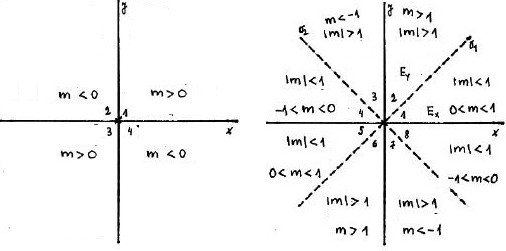
Medzi základné algoritmy rasterizácie úsečky patria tri algoritmy: DDA, Bresenhamov a Midpoint algoritmus. Pri všetkých algoritmoch platí, že vstupom je začiatočný bod $A=(x_A, y_A)$ a koncový bod úsečky $B=(x_B, y_B)$ a výstupom množina bodov rastra, ktoré aproximujú danú úsečku $AB$.