Počítačová grafika

Algoritmus Cohen-Sutherland

Princíp algoritmu

Algoritmus Cohen-Sutherland slúži na orezávanie úsečky do axiálneho okna, ktoré má strany rovnobežné so súradnicovými osami. Algoritmus prebieha počas behu algoritmu a minimalizuje počet orezávaní.

Prvá časť tohto algoritmu slúži na vylúčenie úsečiek, u ktorých netreba počítať prienik s oknom. Takáto úsečka sa buď nachádza celá v okne alebo mimo okna.

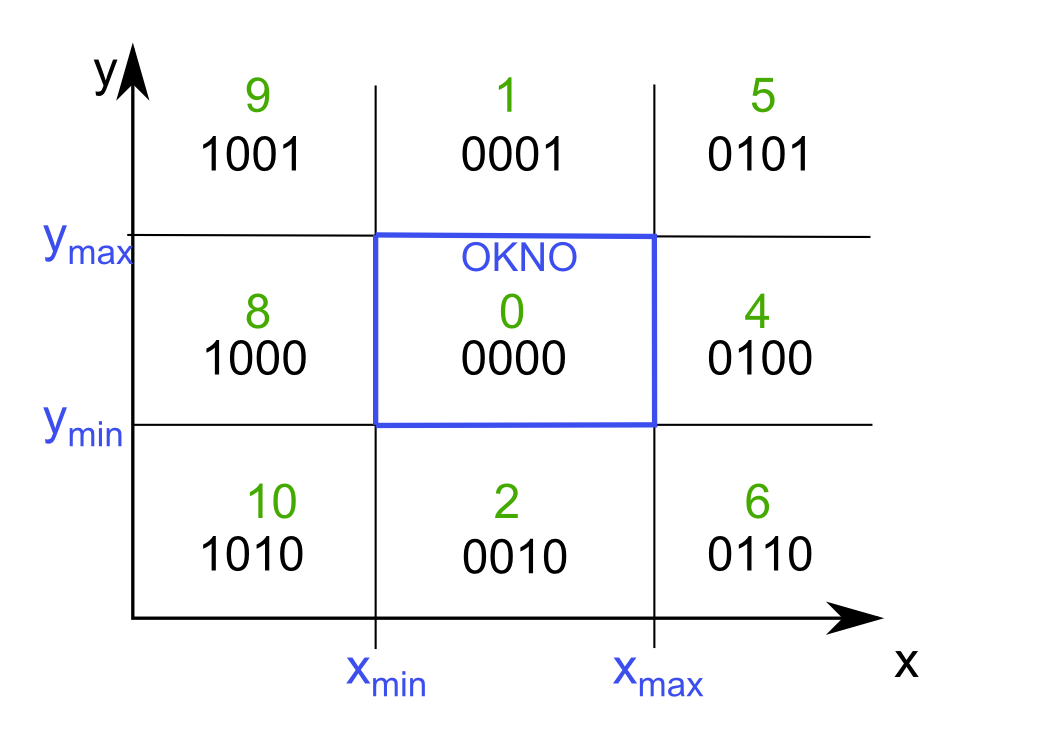
Najprv rozdelíme rovinu na deväť častí hraničnými priamkami okna. Súradnice ($x_{min}$, $x_{max}$, $y_{min}$, $y_{max}$) definujú okno, vzhľadom na ktoré budeme orezávať úsečky. Každej časti priradíme 4-bitový kód, ktorý dostane aj každý bod úsečky, ktorý do tejto oblasti padne (Obr. 1).

Jednotlivé bity pre bod $(x, y)$ sa nastavia nasledovne:

• 1. bit- bod leží naľavo od okna ($x_{min} \gt x$)
• 2. bit- bod leží napravo od okna ($x_{max} \lt x$)
• 3. bit- bod leží nižšie od okna ($y_{min} \gt y$)
• 4. bit- bod leží vyššie od okna ($y_{max} \lt y$)

Preto napríklad bod s kódom 0101 leží napravo a vyššie od okna.

Bod, ktorý sa nachádza vo vnútri okna, má kód 0000. Úsečka je celá v okne a môžeme ju vykresliť, ak oba jej krajné body majú kód 0000. Tento prípad nastane, ak kod(A)||kod(B) = 0000, kde $A$ a $B$ sú krajné body orezávanej úsečky a symbol || predstavuje binárne sčítanie. Takýto test budeme nazývať Trivial accept.

Ďalej môžeme vylúčiť úsečku bez vykreslenia, ak oba jej krajné body sú vľavo, vpravo, hore alebo dole od okna. Ľahko to identifikujeme práve podľa kódov krajných bodov úsečky tak, že urobíme ich logický súčin ((1 and 1)=1, inak 0).

Teda kod(A)& & kod(B) $\neq$ 0000. Takýto test budeme označovať pojmom Trivial reject.

Ak je logický súčin rôzny od 0000, tak úsečka nepretína okno, a teda ju môžeme vylúčiť z vykresľovania. V opačnom prípade úsečku nemôžeme vylúčiť z vykresľovania a musíme ju otestovať na prienik vzhľadom na hranicu okna, v najhoršom prípade 4-krát.

Myšlienku orezávania úsečky $AB$ vzhľadom na axiálne okno môžeme vidieť na Obr. 2.

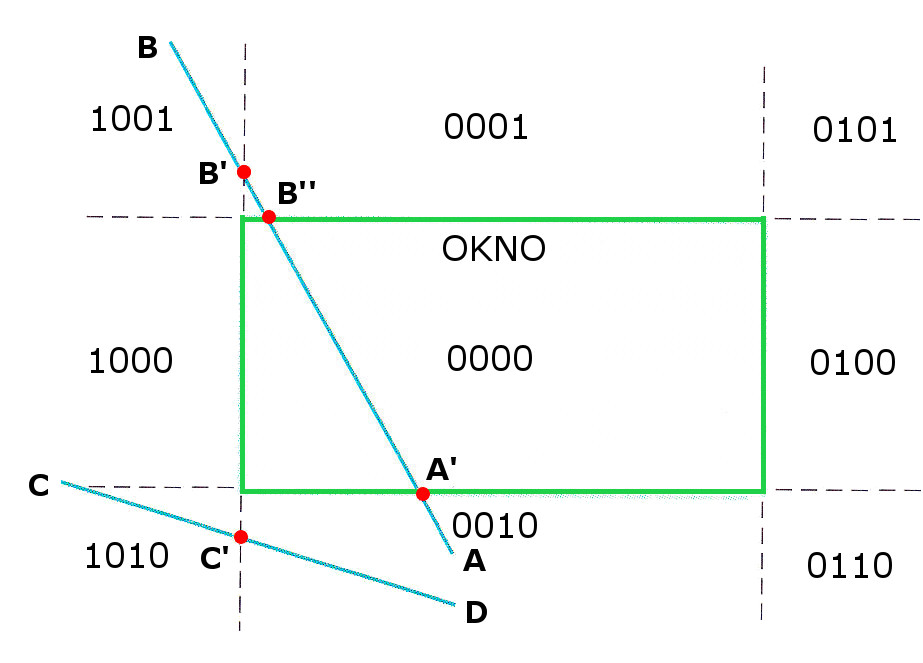
Vyberieme bod mimo okna, napr. bod $A$. Bitový kód bodu $A$ je 0010, preto má zmysel orezávať úsečku $AB$ priamkou prechádzajúcou dolnou hranou okna ($y=y_{min}$). Bod prieniku úsečky a okna označíme ako $A^{'}$. Ten predstavuje nový krajný bod orezávanej úsečky, teda úsečku $ A^{'}B$. Bod $A ^{'}$ sa teraz nachádza na spodnej hrane okna, teda jeho bitový kód predstavuje 0000.

Prechádzame na bod $B$, druhý krajný bod orezávanej úsečky. Z jeho bitového kódu vidíme, že sa nachádza vľavo od okna. Orezávame podľa priamky $x= x_{min}$ a nachádzame bod $B^{'}$. Zahadzujeme pôvodný bod $B$ a nahradíme ho bodom $B^{'}$. Dostávame úsečku $A^{'}B^{'}$.

Z bitového kódu bodu $B^{'}$ vidíme, že sa nachádza nad oknom a preto ho orezávame priamkou $y=y_{max}$. Nachádzame bod $B^{''}$, ktorého bitový kód je 0000. Úspešne sme orezali úsečku $AB$.

V prípade úsečky $CD$ po prvom orezávacom kroku zistíme, že úsečka sa celá nachádza pod/vedľa axiálneho okna, preto ju celú zahadzujeme.

Matematicky je možno vyjadriť prienik orezávanej úsečky s priamkami prechádzajúcimi hranami axiálneho okna pomocou smernicovej rovnice priamky.

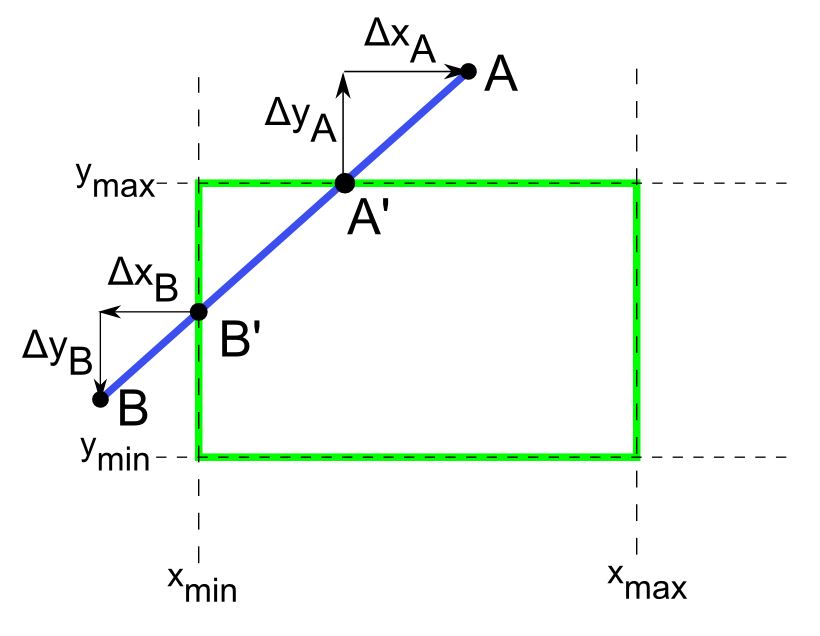
• Orezávanie zľava priamkou $x=x_{min}$ (Obr. 3 ): \begin{equation*} \begin{split} x'_{B}=x_{B}+\Delta x_{B}=x_{B} + (x_{min}-x_{B})=x_{min}, \\ y'_{B}=y_{B}+\Delta y_{B}=y_{B} +\Delta x_{B} \mid m \mid=y_{B} + \mid m \mid (x_{min}-x_{B}) \end{split} \end{equation*}
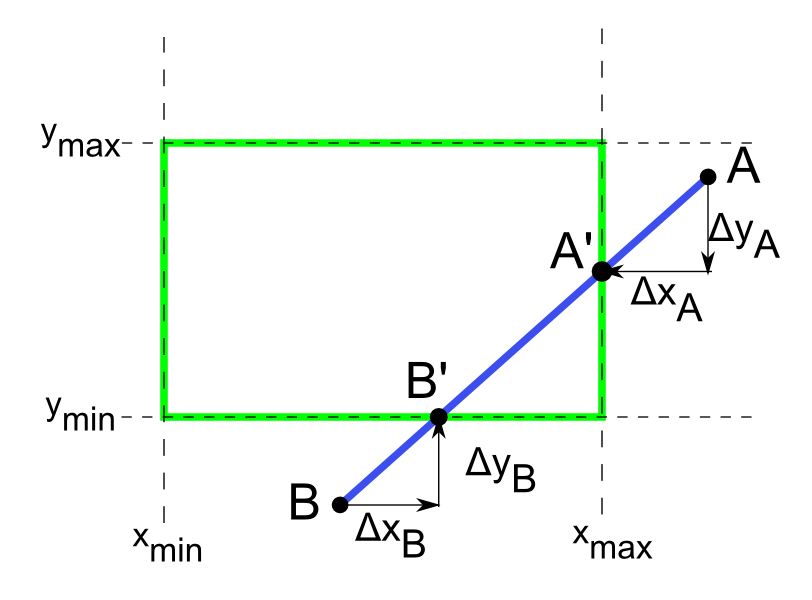
• Orezávanie sprava priamkou $x=x_{max}$ (Obr. 4): \begin{equation*} \begin{split} x'_{A}=x_{A}+\Delta x_{A}=x_{A}+(x_{max}-x_{A})=x_{max}, \\ y'_{A}=y_{A}+\Delta y_{A}=y_{A} +\Delta x_{A} \mid m \mid=y_{A} + \mid m \mid (x_{max}-x_{A}) \end{split} \end{equation*}
• Orezávanie zdola priamkou $y=y_{min}$ (Obr. 4): \begin{equation*} %s hviezdickou sa necisluje \begin{split} x'_{B}=x_{B}+\Delta x_{B}=x_{B}+\dfrac{1}{\mid m \mid}\Delta y_{B}= x_{B}+\dfrac{1}{\mid m \mid}(y_{min}-y_{B}), \\ y'_{B}=y_{B}+\Delta y_{B}=y_{B}+(y_{min}-y_{B})=y_{min} \end{split} \end{equation*}
• Orezávanie zhora priamkou $y=y_{max}$ (Obr. 3): \begin{equation*} %s hviezdickou sa necisluje \begin{split} x'_{A}=x_{A}+\Delta x_{A}=x_{A}+\dfrac{1}{\mid m \mid}\Delta y_{A}= x_{A}+\dfrac{1}{\mid m \mid}(y_{max}-y_{A}), \\ y'_{A}=y_{A}+\Delta y_{A}=y_{A}+(y_{max}-y_{A})=y_{max} \end{split} \end{equation*}

Algoritmus Cohen-Sutherland v danej verzii nevie orezať úsečku rovnobežnú zo súradnicovou osou $y$ podľa axiálneho okna, pretože pre smernicu $m$ takejto úsečky platí $m = \frac{\Delta y}{\Delta x}$, kde $\Delta x = 0$.

Postup výpočtu

Postup orezávania úsečky s krajnými bodmi $A=(x_A, y_A)$ a $B=(x_B, y_B)$ do okna určeného bodmi $M = (x_M, y_M)$ a $N = (x_N, y_N)$.

1. Zisti bitový kód bodu $A$ kod(A) a bitový kod bodu $B$ kod(B).
2. Otestuj Trivial accept bodov $A$ a $B$. Ak vyšlo true vykresli celu úsečku, ak false pokračuj.
3. Otestuj Trivial reject bodov $A$ a $B$.Ak vyšlo true zahoď celu úsečku, ak false pokračuj.
4. Vypočítaj smernicu $m$ úsečky $AB$ ako $m=\frac{y_B-y_A}{x_B-x_A}$ a konštanty $x_{min}=min(x_A,x_B)$, $x_{max}=max(x_A,x_B)$, $y_{min}=min(y_A,y_B)$ a $y_{max}=max(y_A,y_B)$.
5. Vyber krajný bod, ktorý sa nenachádza vnútri axiálneho okna, nech je to bod $A$.
6. Kým $kod1$ bodu $A$ sa nerovná 0000 postupuj:
   1. Orezanie zľava do bodu $A'=(x'_A, y'_A)$: $x'_A=x_{min}$ a $y'_A=y_A+\mid m\mid(x_{min}-x_A)$. Zahoď úsečku $AA'$, teda $A = A'$
   2. Orezanie sprava do bodu $A'=(x'_A, y'_A)$: $x'_A=x_{max}$ a $y'_A=y_A+\mid m\mid(x_{max}-x_A)$. Zahoď úsečku $AA'$, teda $A = A'$
   3. Orezanie zdola do bodu $A'=(x'_A, y'_A)$: $x'_A=x_A+\dfrac{1}{\mid m\mid}(y_{min}-y_A)$ a $y_A=y_{min}$. Zahoď úsečku $AA'$, teda $A = A'$
   4. Orezanie zhora do bodu $A'=(x'_A, y'_A)$: $x'_A=x_A+\dfrac{1}{\mid m\mid}(y_{max}-y_A)$ a $y_A=y_{max}$. Zahoď úsečku $AA'$, teda $A = A'$
7. Vymeň bod $A$ a bod $B$ a opakuj bod 6.

Príklad

Na ilustráciu algoritmu Cohen-Sutherland si ukážeme orezanie úsečky s krajnými bodmi $A = (x_A, y_A)=(0, 0)$ a $B = (x_B, y_B)=(8, 7)$ do axiálneho okna určeného bodmi $M = (x_M, y_M)=(2, 1)$ a $N = (x_N, y_N)=(6, 5)$.

1. Bitový kód bodu $A$ kod(A)=1010 a bitový kod bodu $B$ kod(B)=0101.
2. Trivial accept($A$, $B$) = false.
3. Trivial reject($A$, $B$) = false.
4. $m=\frac{7}{8}$, $x_{min}=min(2,6)=2$, $x_{max}=max(2,6)=6$, $y_{min}=min(1,5)=1$ a $y_{max}=max(1,5)=5$.
5. Vyber krajný bod, nech je to bod $A$.
6. Kým kod(A) bodu $A$ sa nerovná 0000 postupuj:
   • zľava: $x'_A=x_{min}=1$ a $y'_A=0+\frac{7}{8}(2-0)$. Teda $A = (x'_A, y'_A)=(2, \frac{7}{4})$ a kod(A)=0010.
7. Vymeň bod $A$ a bod $B$, teda $A=(8, 7)$ a $B=(2, \frac{7}{4})$. V tomto prípade kod(A)=0101
   • sprava: $x'_A=x_{max}=6$ a $y'_A=7+\dfrac{7}{8}(6-8)$. Teda $A = (x'_A, y'_A)=(6, \frac{21}{4})$ a kod(A)=0001.
   • zhora: $x'_A=6+\dfrac{8}{7}(5-\frac{21}{4})=\frac{40}{7}$ a $y_A=5$. Teda $A = (x'_A, y'_A)=(\frac{40}{7}, 5)$ a kod(A)=0000.
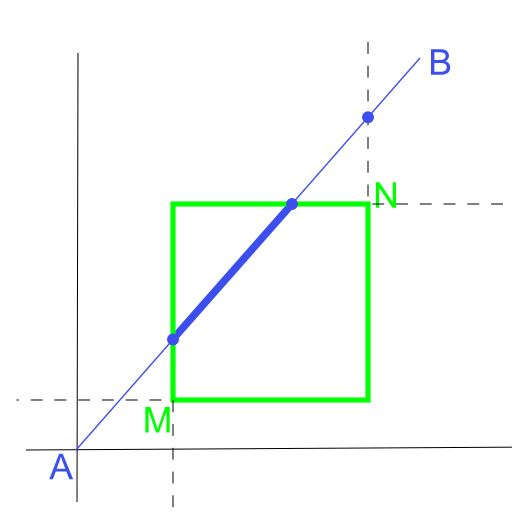
8. Algoritmus končí. Krajné body orezanej úsečky sú $A = (\frac{40}{7}, 5)$, $B=(2, \frac{7}{4})$. Výslednú orezanú úsečku môžete vidieť na Obr. 5.

Ďalšie riešené a neriešené príklady.

Interaktívny applet

Pseudokód

Implementácia algoritmu Cohen-Sutherland je zhrnutá v nasledujúcom pseudokóde.

Na vstupe sú dva krajné body úsečky $A=(x_{A},y_{A})$ a $B=(x_{B},y_{B})$. Súradnice ( $x_{min}$, $x_{max}$, $y_{min}$, $y_{max}$) definujú okno, podľa ktorého orezávame úsečku.

Procedúra $ZistiKod(x, y, kod)$, priradí premennej $kod$ 4-bitový kód bodu $(x,y)$.

Procedúra TrivialAccept(kod1, kod2) porovná bitové kódy dvoch rôznych bodov kod1 a kod2. Vráti hodnotu true, ak sa oba body nachádzajú vnútri okna a false ak nie.

Procedúra TrivialReject(kod1, kod2) porovná bitové kódy dvoch rôznych bodov kod1 a kod2. Vráti hodnotu true, ak sa oba body nachádzajú vľavo/vpravo/zľava alebo sprava od okna a false ak nie.

Funkcia ROUND(x) predstavuje zaokrúhlenie hodnoty $x$ na celé čísla.

Literatúra

Algoritmus Cohen-Sutherland vieme nájsť podrobne spracovaný v anglickej literatúre [3] od strany 226.

S jeho vysvetlením sa môžeme stretnúť aj v [1] o strany 26 a v českej literatúre [2] sú tomuto algoritmu venované dve strany 106-107.