Počítačová grafika

Bresenhamov stredový kružnicový algoritmus (Midpoint Circle Algorithm)

Princíp algoritmu

Algoritmus predstavuje úpravu Bresenhamovho midpoint line algoritmu pre kružnicu. Vychádza z polomeru $r$ kružnice $K$ a jej stredu v začiatku súradnicovej sústavy, t.j. v bode $(x_C,y_C)=(0,0)$.

Ak sa stred $(x_C,y_C)$ nenachádza v začiatku, tak pozíciu bodu kružnice $(x,y)$ vieme vypočítať pričítaním $x_C$ k $x$-ovej súradnici a $y_C$ k $y$-ovej. Vychádzame z rovnice kružnice: $f(x,y)=x^2+y^2-r^2=0$.

Platí

• Ak $f(x,y) \lt 0$, tak bod $(x,y)$ sa nachádza vnútri kružnice $K$. Takýto bod nazývame vnútorný bod
• Ak $f(x,y) = 0$, tak bod $(x,y)$ sa nachádza na kružnici $K$
• Ak $f(x,y) \gt 0$, tak bod $(x,y)$ sa nachádza mimo kružnice $K$. Takýto bod nazývame vonkajší bod.

Opäť sa nachádzame na segmente kružnice od bodu $(0,r)$ až po bod, pre ktorý je $x_i \geq y_i$ Nech sme v bode $(x_i,y_i)$ a hľadáme nasledujúci bod. Rozhodujeme sa medzi dvoma kandidátmi $E=(x_i+1,y_i)$ a $SE=(x_i+1,y_i-1)$ (Obr. 1).

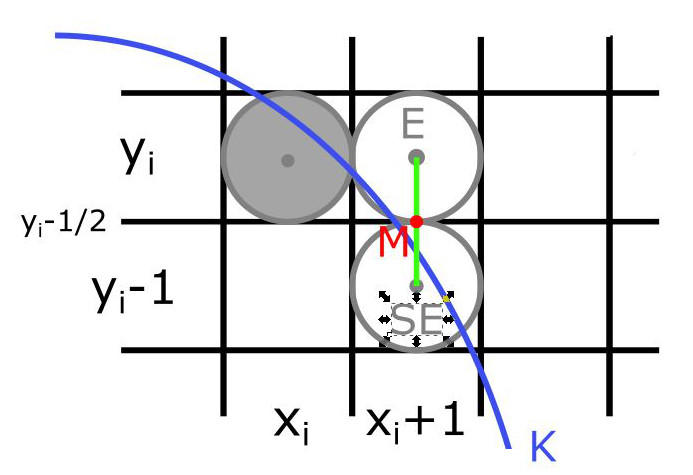
Určíme $M=stred(E,SE)=(x_i+1,y_i-\frac{1}{2})$. Budeme zisťovať, či tento bod je vnútorný alebo vonkajší. Definujeme rozhodovací parameter $p_i$:

$p_i=f(M)=(x_i+1)^2+(y_i-\frac{1}{2})^2-r^2$ a odvodíme z neho rekurentný vzorec: $p_{i+1}=f((x_{i+1}+1,y_{i+1}-\frac{1}{2})=(x_{i+1}+1)^2+(y_{i+1}-\frac{1}{2})^2-r^2$

Potom $p_{i+1}-p_i=2x_{i+1}+(y_{i+1}^2-y_{i+1})-(y_{i}^2-y_i)+1$ rekurentný predpis má tvar: $p_{i+1}=p_i+2x_{i+1}+(y_{i+1}^2-y_{i+1})-(y_i^2-y_i)+1$

Zrejme platí:

• Ak $p_i \lt 0$, vyberáme ako nasledujúci pixel $(x_{i+1},y_{i+1})=E=(x_i+1,y_i)$ a $p_{i+1}=p_i+2x_i+3$
• Ak $p_i \geq 0$, vyberáme bod $(x_{i+1},y_{i+1})=SE=(x_i+1,y_i-1)$ a teda $p_{i+1}=p_i+2(x_i-y_i)+5$

Potrebujeme ešte poznať hodnotu začiatočného parametra $p_0=(x_0+1)^2+(y_0-\frac{1}{2})^2-r^2$, ktorý pre bod $(x_0,y_0)=(0,r)$ sa rovná $p_0=\frac{5}{4}-r$. Ak je polomer špecifikovaný ako celé číslo, môžeme hodnotu $p_0$ zaokrúhliť ako $p_0=1-r$, lebo všetky prírastky sú celočíselné.

Na rozdiel od lineárnych algoritmov rasterizácie úsečky, sme v prípade kružnicových algoritmov nezískali rovnaké rozhodovacie parametre.

Postup algoritmu sme ilustrovali pre kružnicový oblúk, ktorý sa nachádza v II. oktante, avšak algoritmus je možné rovnakým spôsobom odvodiť aj pre ktorýkoľvek z ostatných oktantov. Podobne ako Bresenhamov line algoritmus, aj tento vypočítava pixely pozdĺž kružnice, používajúc pri tom len celočíselné sčítania a odčítania za predpokladu, že stred a polomer kružnice sú špecifikované v celočíselných obrazových súradniciach.

Postup výpočtu

Kroky algoritmu vieme zhrnúť nasledovne:

1. Zadaj polomer $r$ a stred kružnice $(x_C,y_C)$ a urči prvý bod na kružnici so stredom v začiatku $(x_0 ,y_0)=(0, r)$.
2. Vypočítaj začiatočnú hodnotu rozhodovacieho parametra ako $p_0 =1-r$ (pretože predpokladáme, že $r$ je celočíselné).
3. V každej pozícii $x_i$, štartujúc v $i=0$, vykonaj nasledujúci test:
   1. Ak $p_i \lt 0$: nasledujúci bod pozdĺž kružnice so stredom $(0,0)$ bude $(x_{i+1}, y_{i+1})=(x_i+1,y_i)$ a $p_{i+1}=p_i+2x_i+3$.
   2. Inak je nasledujúci bod $(x_{i+1}, y_{i+1})=(x_i+1,y_i-1)$ a $p_{i+1}=p_i+2(x_i-y_i)+5$.
4. Urči súmerné body v ostatných siedmich oktantoch.
5. Posuň každú vypočítanú pixlovú pozíciu $(x, y)$ na kružnicu so stredom $(x_C ,y_C )$ a zobraz bod so súradnicami: $x=x+x_C$,$y=y+y_C$.
6. Opakuj kroky 3. až 5. pokiaľ $x_i \geq y_i$.

Príklad

Na ilustráciu algoritmu si ukážeme rasterizáciu kružnice so stredom v bode $(x_C, y_C)=(1, 2)$ a polomerom $r=7$.

1. $(x_0,y_0)=(0,r)=(0,7)$
2. $p_0=1-r=-6$
3. • $i=0:$ $p_0 \lt 0 \Rightarrow (x_1,y_1)=(x_0+1,y_0)=(1,7)$ a $p_1=p_0+2x_0+3=-3$
   • $i=1:$ $p_1 \lt 0 \Rightarrow (x_2,y_2)=(x_1+1,y_1)=(2,7)$ a $p_2=p_1+2x_1+3=2$
   • $i=2:$ $p_2 \gt 0 \Rightarrow (x_3,y_3)=(x_2+1,y_2-1)=(3,6)$ a $p_3=p_2+2(x_2-y_2)+5=-3$
   • $i=3:$ $p_3 \lt 0 \Rightarrow (x_4,y_4)=(x_3+1,y_3)=(4,6)$ a $p_4=p_3+2x_3+3=6$
   • $i=4:$ $p_4 \gt 0 \Rightarrow (x_5,y_5)=(x_4+1,y_4-1)=(5,5)$ a $x_5\geq y_5$ teda algoritmus končí.
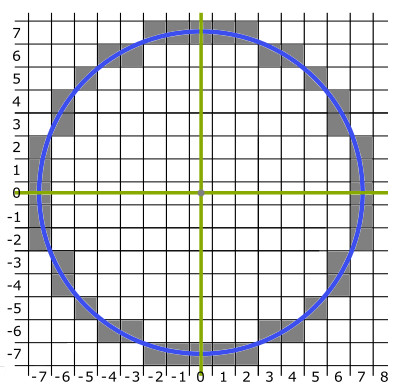
4. Určíme súmerne položené body v ostatných oktantoch (Obr. 2).
5. Posunieme každú hodnotu pixla do stredu $(1,2)$. Teda body: $(2,9),(3,9),(4,8),(5,8),(6,8), ...$

Ďalšie riešené a neriešené príklady.

Interaktívny applet

Pseudokód

Implementácia Bresenhamovho stredového kružnicového algoritmu je zhrnutá v nasledujúcom pseudokóde. Na vstupe je stred kružnice $(x_C,y_C)$ a polomer kružnice $r$.

Literatúra

Bresenhamov stredový kružnicový algoritmus je detailne spracovaný v knihe [3] od strany 98. Zo slovenskej/českej literatúry nie je uvedený ani v [1] ani v [2].