Počítačová grafika

Algoritmus Liang-Barsky

Princíp algoritmu

Algoritmus Liang-Barsky slúži na orezávanie úsečky do konvexného mnohouholníka. Bod na úsečke $AB$ je reprezentovaný pomocou parametrického vyjadrenia úsečky, \begin{equation} P(\alpha) = (1-\alpha)A+\alpha B, \end{equation} kde $0\leq\alpha\leq 1$.

Algoritmus počíta dve hodnoty parametra $\alpha_{0}$, $\alpha_{1}$, ktorým prislúcha výsledná orezaná úsečka $P(\alpha_{0}) P(\alpha_{1})$, kde $\alpha_{0} \lt \alpha_{1}$ (Obr. 1).

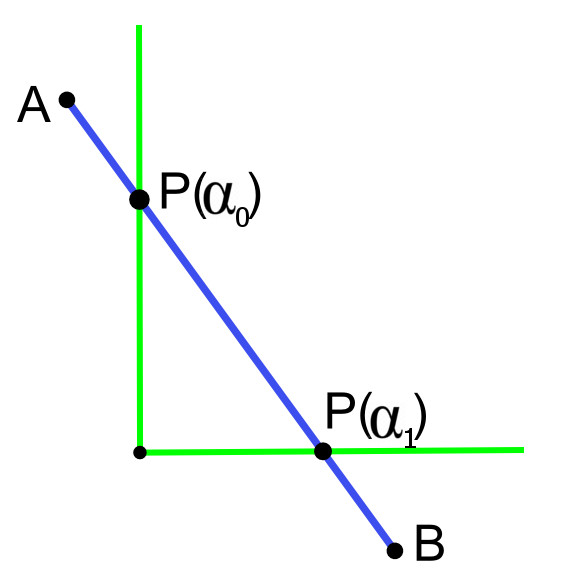
Na začiatku algoritmu sa inicializujú hodnoty ako $\alpha_{0}=0$ a $\alpha_{1}=1$, teda $P(\alpha_{0}) P(\alpha_{1})=AB$.

K orezávaniu úsečky pristupujeme postupne vzhľadom na polroviny mnohouholníka. Skúmame, ako oreže úsečku polrovina určená $\lt R, \textbf{n} \gt$, kde $\textbf{n}$ je normálový vektor hranice smerujúci dovnútra polroviny (Obr. 2).

Počas priebehu algoritmu bude hodnota $\alpha_{0}$ rásť (neklesať) a hodnota $\alpha_{1}$ klesať (nerásť). Ak $\alpha_{0} \gt \alpha_{1}$, tak orezávaná úsečka je prázdna a algoritmus končí.

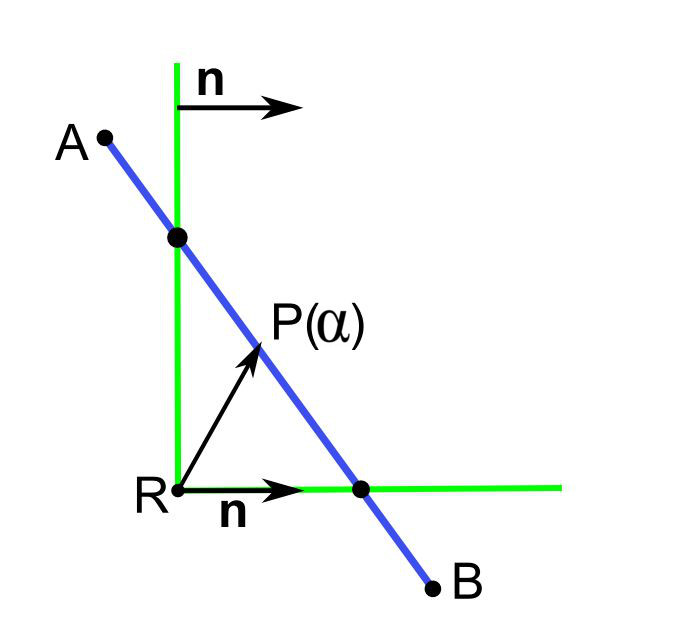
Potrebujeme zistiť hodnotu $\alpha$ (ak existuje), pre ktorú priamka, na ktorej leží úsečka, pretína hranicu polroviny. Presnejšie potrebujeme nájsť podmienku, aby $P(\alpha)$ patril polrovine. Aby sme takéto $\alpha$ vypočítali, dosadíme $P(\alpha)$ do podmienky patriť polrovine: \begin{equation} \begin{split} (P(\alpha)-R).\textbf{n}\geq 0,\\ ((1-\alpha)A+\alpha B) - R).\textbf{n} \geq 0,\\ (A+\alpha (B - A)) - R).\textbf{n} \geq 0,\\ \alpha(B - A).\textbf{n} + (A - R).\textbf{n} \geq 0,\\ \alpha(B - A).\textbf{n} \geq (R - A).\textbf{n},\\ \alpha d_l \geq d_r, \end{split} \end{equation} kde $d_l = (B-A).\textbf{n}$ a $d_r = (R-A).\textbf{n}$ (Obr. 2).

Potom existuje niekoľko prípadov v závislosti od hodnoty $d_l$:

• $d_l \gt 0$: Potom $\alpha \geq\frac{d_r}{d_l}$. Aby sme to zabezpečili, stačí položiť: $\alpha_0 = max(\alpha_0,\frac{d_r}{d_l})$.Ak je $\alpha_0 \gt \alpha_1$ ako výsledok dostaneme, že orezávaná úsečka je prázdna a algoritmus končí.
• $d_l \lt 0$: Potom $\alpha \leq\frac{d_r}{d_l}$. Aby sme to zabezpečili, stačí položiť: $\alpha_1 = min(\alpha_1,\frac{d_r}{d_l})$. Ak ako výsledok dostaneme $\alpha_0 \gt \alpha_1$, tak opäť orezávaná úsečka je prázdna a algoritmus končí.
• $d_l = 0$: Potom $\alpha$ nie je definované. Geometricky to znamená, že hraničná priamka a orezávaná úsečka sú rovnobežné. V tomto prípade stačí vziať ľubovoľný bod na úsečke napr. $A$ a ak bude $(A-R).\textbf{n} \lt 0$, tak bude jasné, že celá úsečka je mimo polroviny, a preto prienik s mnohouholníkom je prázdny. Inak neurobíme nič, čiže pokračujeme v orezávaní ďalšími polrovinami.

Vo všeobecnosti je algoritmus Liang-Barsky efektívnejší ako algoritmus Cohen-Sutherland, pretože netreba počítať prienik úsečky a okna. Každá aktualizácia parametru $u$ vyžaduje iba operáciu delenia a prienik úsečky a okna sa počíta iba jedenkrát.

Taktiež Cohen-Sutherland môže hľadať prienik okna s úsečkou aj keď tá sa nachádza mimo okna. Oba tieto algoritmy je možné rozšíriť do trojdimenzionálneho priestoru.

Postup výpočtu

Na ilustráciu algoritmu Liang-Barsky si ukážeme orezanie úsečky s krajnými bodmi $A = (x_A, y_A)$ a $B = (x_B, y_B)$. Je dané okno, kde $x \in \lt x_{min},x_{max} \gt $ a $y \in \lt y_{min},y_{max} \gt $. Určenie polrovín si vyžaduje voľbu minimálne dvoch bodov, $R_0 = (x_{min}, y_{min})$ a $R_1 = (x_{max}, y_{max})$ a dvoch vektorov $\boldsymbol{e_x} = (1, 0)$ a $\boldsymbol{e_y} = (0, 1)$.

1. Vytvoríme nasledujúce štyri polroviny: \begin{equation*} \begin{aligned}[c] H_1= \langle R_0, \boldsymbol{e_x} = (1, 0)\rangle;\\ H_2= \langle R_0, \boldsymbol{e_y} = (0, 1)\rangle\\ \end{aligned} \qquad \qquad \begin{aligned}[c] H_3= \langle R_1, \boldsymbol{-e_x} = (-1, 0)\rangle\\ H_4= \langle R_1, \boldsymbol{-e_y} = (0, -1)\rangle\\ \end{aligned} \end{equation*}
2. Inicializácia $\alpha_{0}=0$ a $\alpha_{1}=1$.
3. Pre každú polrovinu $H= \langle R, \boldsymbol{n}\rangle$;
   1. Vypočítaj $d_l = (B-A).\textbf{n}$ a $d_r = (R-A).\textbf{n}$
   2. Ak $d_l \gt 0$, tak $\alpha \geq\frac{d_r}{d_l}$ a $\alpha_0 = max(\alpha_0,\frac{d_r}{d_l})$.
   3. Ak $d_l \lt 0$, tak $\alpha \leq\frac{d_r}{d_l}$ a $\alpha_1 = min(\alpha_1,\frac{d_r}{d_l})$.
   4. Ak $d_l = 0$, tak $\alpha$ nie je definované. Ak $(A-R).\textbf{n} \lt 0$, a úsečka je mimo polroviny, a preto prienik s mnohouholníkom je prázdny. Inak pokračujeme v orezávaní ďalšími polrovinami.
   5. Ak je $\alpha_0 \gt \alpha_1$ ako výsledok dostaneme, že orezávaná úsečka je prázdna a algoritmus končí
4. Krajné body orezanej úsečky sú:
   • $A = P(\alpha_0) = (1-\alpha_0)A+\alpha_0 B$
   • $B = P(\alpha_1) = (1-\alpha_1)A+\alpha_1 B$

Príklad

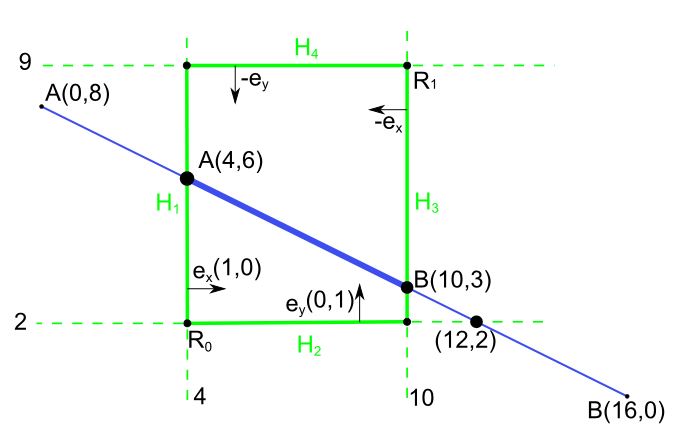
Na ilustráciu algoritmu Liang-Barsky si ukážeme orezanie úsečky s krajnými bodmi $A = (x_A, y_A)=(0, 8)$ a $B = (x_B, y_B)=(16, 0)$.

Je dané okno, kde $x \in \lt 4,10 \gt$ a $y \in \lt 2,9 \gt$. Určenie polrovín si vyžaduje voľbu minimálne dvoch bodov, $R_0 = (4, 2)$ a $R_1 = (10, 9)$ a dvoch vektorov $\boldsymbol{e_x} = (1, 0)$ a $\boldsymbol{e_y} = (0, 1)$.

1. Vytvoríme nasledujúce štyri polroviny: \begin{equation*} \begin{aligned}[c] H_1= \langle R_0 = (4, 2,), \boldsymbol{e_x} = (1, 0)\rangle;\\ H_2= \langle R_0 = (4, 2,), \boldsymbol{e_y} = (0, 1)\rangle\\ \end{aligned} \qquad \qquad \begin{aligned}[c] H_3= \langle R_1 = (10, 9), \boldsymbol{-e_x} = (-1, 0)\rangle\\ H_4= \langle R_1 = (10, 9), \boldsymbol{-e_y} = (0, -1)\rangle\\ \end{aligned} \end{equation*}
2. Inicializácia $\alpha_{0}=0$ a $\alpha_{1}=1$.

3. $ H_1=\langle R_0, \boldsymbol{e_x}\rangle$:

   $d_l = (B-A).\boldsymbol{e_x}=(16,-8).(1,0)=16 \gt 0$

   $d_r = (R_0-A)\boldsymbol{e_x}=(4,-6).(1,0)=4\Rightarrow \alpha \geq \frac{1}{4} $

   $d_l \gt 0: \alpha_0 = max(0, \frac{1}{4})= \frac{1}{4}$

   Čiastkový výsledok: $(\alpha_0=\frac{1}{4}, \alpha_1=1)$

4. $ H_2=\langle R_0, \boldsymbol{e_y}\rangle$:

   $d_l = (B-A).\boldsymbol{e_y}=(16,-8).(0,1)=-8 \lt 0$

   $d_r = (R_0-A)\boldsymbol{e_y}=(4,-6).(0,1)=-6\Rightarrow \alpha \leq \frac{3}{4} $

   $d_l \lt 0: \alpha_1 = min(1, \frac{3}{4})= \frac{3}{4}$

   Čiastkový výsledok: $(\alpha_0=\frac{1}{4}, \alpha_1=\frac{3}{4})$

5. $ H_3=\langle R_1, \boldsymbol{-e_x}\rangle$:

   $d_l = (B-A).\boldsymbol{-e_x}=(16,-8).(-1,0)=-16 \lt 0$

   $d_r = (R_1-A).\boldsymbol{-e_x}=(10,1).(-1,0)=-10\Rightarrow \alpha \leq \frac{5}{8} $

   $d_l \lt 0: \alpha_1 = min(\frac{3}{4}, \frac{5}{8})= \frac{5}{8}$

   Čiastkový výsledok: $(\alpha_0=\frac{1}{4}, \alpha_1=\frac{5}{8})$

6. $ H_4=\langle R_1, \boldsymbol{-e_y}\rangle$:

   $d_l = (B-A).\boldsymbol{-e_y}=(16,-8).(0,-1)=8 \gt 0$

   $d_r = (R_1-A).\boldsymbol{-e_y}=(10,1).(0,-1)=-1\Rightarrow \alpha\geq -\frac{1}{8} $

   $d_l \gt 0: \alpha_0 = max(\frac{1}{4}, -\frac{1}{8})= \frac{1}{4}$

7. Výsledok je $(\alpha_0=\frac{1}{4}, \alpha_1=\frac{5}{8})$. Teda krajné body orezanej úsečky sú:
   • Pre $\alpha_0=\frac{1}{4}:\frac{3}{4}(0,8)+\frac{1}{4}(16,0)=(4,6)=A$
   • Pre $\alpha_1=\frac{5}{8}:\frac{3}{8}(0,8)+\frac{5}{8}(16,0)=(10,3)=B$

Ďalšie riešené a neriešené príklady.

Interaktívny applet

Literatúra

Algoritmus Liang-Barsky vieme nájsť podrobne spracovaný v anglickej literatúre [3] od strany 230. Zo slovenskej a českej literatúry sa nenachádza v [1] ani v [2].