Orezávanie
Algoritmy na orezávanie bodu
Predpokladáme, že máme bod $A=(x_A,y_A)$ a okno, vzhľadom na ktoré orezávame je dané svojimi min-max súradnicami $x_{min}, x_{max}, y_{min}, y_{max}$.
Ak bod spĺňa všetky nerovnosti nižšie, bod leží v okne a vykreslíme ho. Inak tento bod zahadzujeme.
\begin{equation} \begin{split} x_{min} \leq x_A \leq x_{max}\\ y_{min} \leq y_A \leq y_{max} \end{split} \end{equation}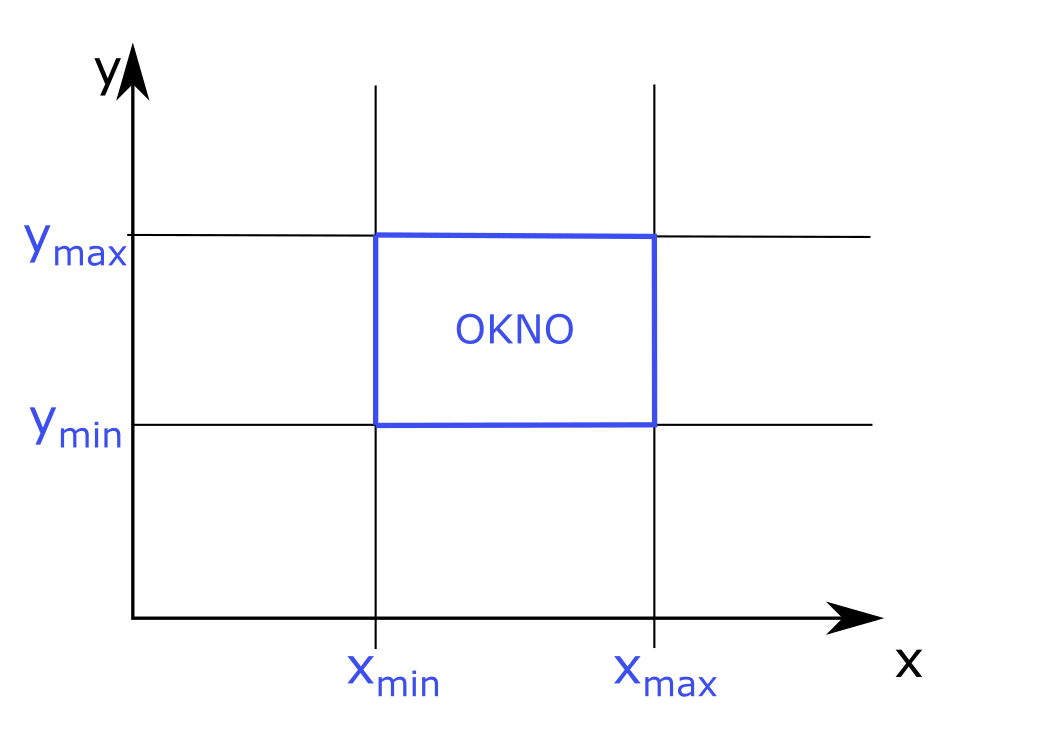
Algoritmy na orezávanie úsečky do axiálneho okna
Orezávanie bodu je pomerne jednoduché. Na zložitejšie objekty však potrebujeme viac operácií, a preto sa snažíme ich počet minimalizovať. Tak je to aj s úsečkou vo všeobecnej polohe. Najprv otestujeme jej krajné body, a ak patria do okna, tak aj úsečka leží v okne.
V prípade, že úsečka neleží v okne, otestujeme jej prienik s oknom. Ak úsečka pretína okno, tak ju orezávame, a na to potrebujeme zistiť body prieniku ( t.j. kde úsečka pretne hranice okna).
Podstatnou vlastnosťou pri orezávaní je rýchlosť algoritmu na nájdenie bodov prieniku (pri vykresľovaní scény môžeme mať rádovo tisíce objektov, ktoré treba orezať, za čo najkratší čas). Preto vzniklo niekoľko algoritmov na orezávanie. Najprv ale musíme urobiť testy, či naozaj treba hľadať body prieniku. Úsečky, ktoré ležia v okne, orezávať netreba, tie môžeme rovno vykresliť. Ak oba krajné body úsečky ležia nad oknom, t.j. majú súradnicu $y$ > $y_{max}$ okna, tak úsečku nevykreslíme. Podobne ak oba krajné body úsečky ležia pod oknom, naľavo či napravo od okna, tak úsečku nevykreslíme.
V tejto kapitole si predstavíme jeden algoritmus na orezávanie úsečky - algoritmus Cohen-Sutherland.