Počítačová grafika

Bresenhamov algoritmus rasterizácie úsečky (Bresenham's Line Algorithm)

Princíp algoritmu

Tento algoritmus vykresľuje body rastra, ktoré ležia najbližšie ku geometrickému obrazu úsečky v zvislom/vodorovnom smere. Využíva sa výhradne celočíselná aritmetika.

Ilustrujeme postup pre časť úsečky $AB$ (bod $A$ leží naľavo od bodu $B$), ak riadiacou osou je $x$-ová súradnicová os a pre smernicu tejto úsečky $AB$ platí $0 \lt m \lt 1$. Prírastok v smere osi $x$ sa konštantne zväčšuje o hodnotu $+1$ (Obr. 1).

Predpokladajme, že sme v pozícii bodu úsečky $X=(x_i,y_i)$. Vzhľadom na jednotkové krokovanie v smere osi $x$, kandidátmi na ďalší bod sú pixely $E=(x_i+1,y_i)$ alebo $NE=(x_i+1,y_i+1)$. Je to ten z nich, ktorý je bližšie ku geometrickému priesečníku $P$ danej úsečky so spojnicou týchto pixlov. Označíme $d_1=y-y_i$ a $d_2=(y_i+1)-y$, kde $y$ je $y$-ová súradnica bodu $P$ na priamke a teda platí $y=m(x_i+1)+b$ (Obr. 1). Z toho $d_1=m(x_i+1)+b-y_i$ a $d_2=(y_i+1)-m(x_i+1)+b$.

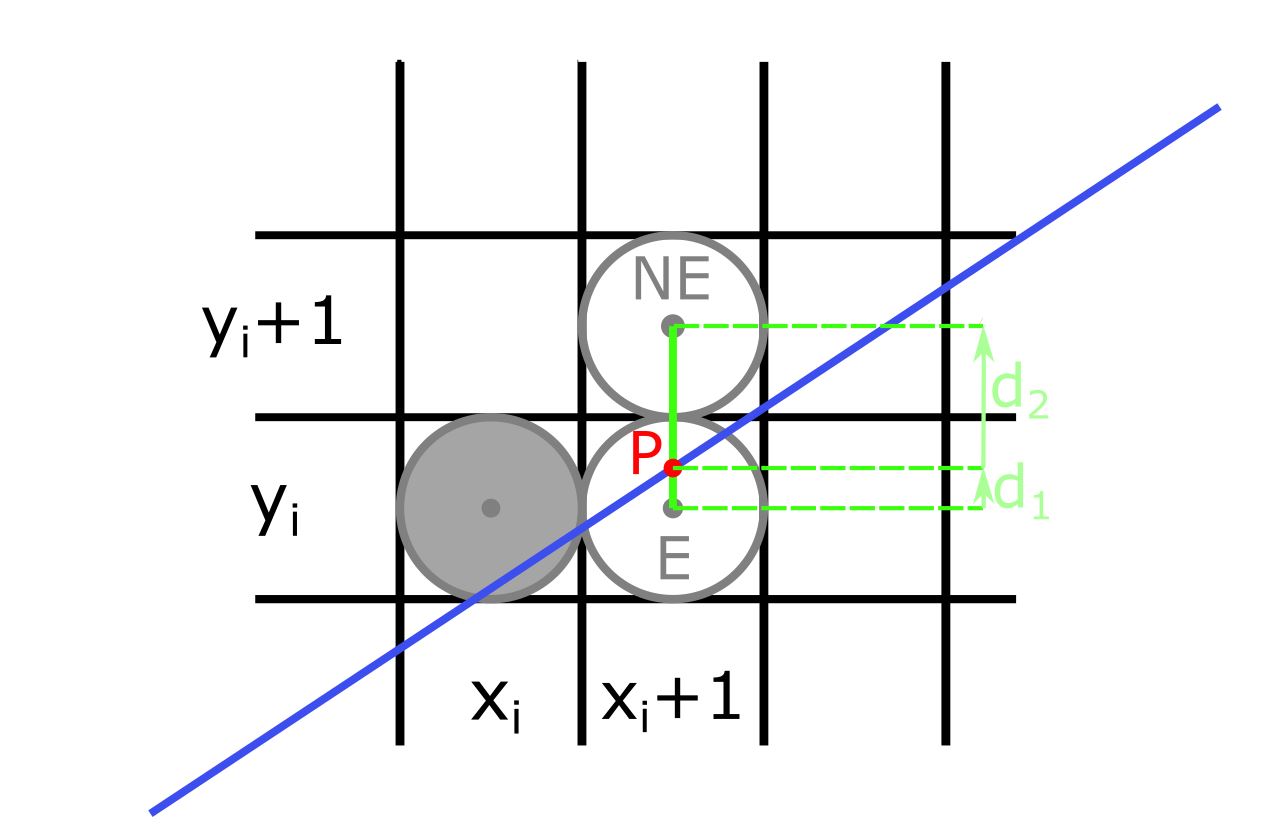
Zvolíme si premennú $\Delta d=d_1-d_2=2m(x_i+1)-2y_i+2b-1$, podľa ktorej vieme určiť, ktorý z dvoch možných pixlov je bližšie k úsečke $AB$. Je zrejmé, že:

• Ak $\Delta d \lt 0 \Leftrightarrow d_1 \lt d_2$, tak bližšie k úsečke je pixel $E=(x_i+1,y_i)$.
• Ak $\Delta d \gt 0 \Leftrightarrow d_1 \gt d_2$, tak bližšie je pixel $NE=(x_i+1,y_i+1)$.
• V prípade, ak $\Delta d=0 \Leftrightarrow d_1=d_2$, je jedno, ktorý z týchto pixlov sa vykreslí, obyčajne ten s väčšou $y$-ovou súradnicou.

Z uvedeného postupu vyplýva, že pre určenie, ktorý pixel sa vykreslí, nie je dôležité vypočítať hodnotu premennej $\Delta d$, ale iba určiť jej znamienko. Preto pri rozhodovaní môžeme túto hodnotu nahradiť ľubovoľným jej kladným násobkom, konkrétne parametrom $p_i=dx \Delta d$. Týmto krokom prenesieme výpočet do celočíselnej aritmetiky, pretože tým eliminujeme jediný neceločíselný člen, smernicu $m=\frac{dy}{dx}$.

Pre zjednodušenie výpočtov je vhodné si vyjadriť parameter $p_i$ rekurentne:

• $p_i=2dy x_i-2dx y_i + C$, kde $C=2dy+dx(2b-1)$ je konštanta nezávislá od $i$.
• $p_{i+1}=2dy x_{i+1}-2dx y_{i+1} + C$

Z toho: $p_{i+1}-p_i=-2 dx(y_{i+1}-y_i)+2 dy\Rightarrow p_{i+1}=p_i-2 dx(y_{i+1}-y_i)+2 dy$. Aby sme mohli tento predpis využiť, potrebujeme ešte hodnotu $p_0=2dy-dx$, kde sme pri výpočte využili, že $y_0$ je bod na priamke a platí $y_0=mx_0+b$. Teraz môžeme iteračným spôsobom počítať hodnoty každého nasledujúceho parametra $p$ z jeho predchádzajúcej hodnoty. Teda:

• Ak $p_i \lt 0\Leftrightarrow d_1 \lt d_2$, tak vykreslíme bod na pozícií $E=(x_i+1,y_i)$, t.j. $y_{i+1}=y_i$ a teda $p_{i+1}=p_i+2 dy$
• Ak $p_i\geq 0\Leftrightarrow d_1 \gt d_2$, tak vykreslíme bod na pozícií $NE=(x_i+1,y_i+1)$, t.j. $y_{i+1}=y_i+1$ a teda $p_{i+1}=p_i+2(dy -dx)$

Všeobecne:

Vo vyššie opísanom postupe sme predpokladali, že smernica $0 \lt m \lt 1$ a teda $x_{i+1}=x_i+1$. Ak pre smernicu $m$ platí $-1 \lt m \lt 0$, tak sa jednotkový krok na $x$-ovej osi zmení na $-1$, teda $x_{i+1}=x_i-1$.

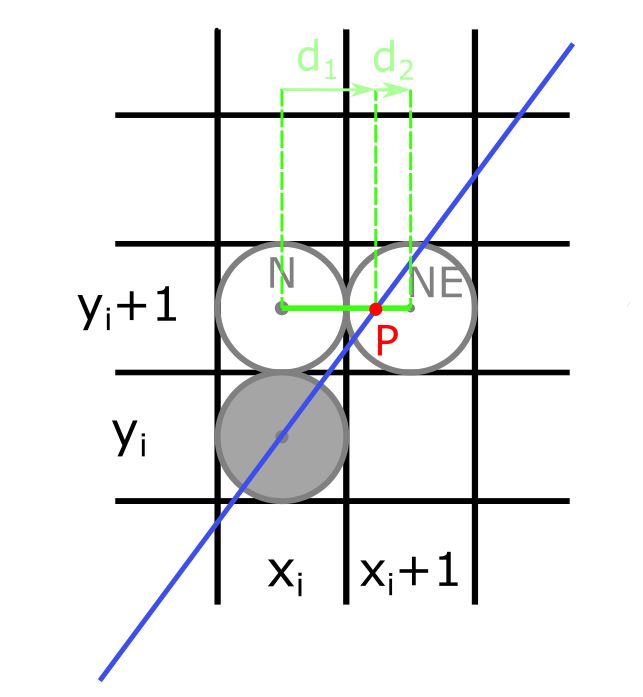
Princíp algoritmu je rovnaký aj pre úsečku $AB$ so smernicou $m \gt 1$.Vtedy sa bod $A$ nachádza nižšie ako bod $B$, t.j. $y_A \lt y_B$ (Obr. 2). Úsečka je priklonená k osi $y$. Preto zvolíme vzorkovanie v smere osi $y$ o hodnotu +1. Ak sa nachádzame v pixli $X=(x_i,y_i)$, tak kandidáti na vykreslenie sú na pozícii $N=(x_i,y_i+1)$ a $NE=(x_i+1,y_i+1)$. Označíme $P$ geometrický priesečník danej úsečky so spojnicou týchto pixlov. Hodnoty $d_1$ a $d_2$ reprezentujú vzdialenosť medzi priesečníkom $P$ a stredom pixlov $N$ a $NE$ (Obr. 2). Teda $d_1=x-x_i$ a $d_2=x_{i+1}-x$, kde $x$ je $x$-ová súradnica bodu $P$ a zo smernicovej rovnice priamky pre ňu dostaneme $x=\frac{1}{m}(y_{i+1}-b)$.

Parameter $p_i$ je možné určiť ako $p_i=dy (d_1-d_2)=2 dx y_i-2 dy x_i + C$, kde $C=2dx(1-b)-dy$ je konštanta nezávislá od $i$. Potom $p_{i+1}=p_i+2dx -2dy(x_{i+1}-x_i)$ a $p_0=2dx-dy$

Teda pre vzorkovanie v smere osi $y$ platí:

• Ak $p_i \lt 0\Leftrightarrow d_1 \lt d_2$, tak vykreslíme bod na pozícií $N=(x_i,y_i+1)$, t.j. $x_{i+1}=x_i$ a $p_{i+1}=p_i+2 dx$
• Ak $p_i\geq 0\Leftrightarrow d_1 \gt d_2$, tak vykreslíme bod na pozícií $NE=(x_{i+1},y_{i+1})$, t.j. $x_{i+1}=x_i+1$ a $p_{i+1}=p_i+2(dx -dy)$

Postup výpočtu pre $0 \lt m \lt 1$

1. Vlož dva krajné body $(x_A, y_A)$ a $(x_B, y_B)$ a zober ľavý (s menšou $x$-ovou súradnicou) ako bod $(x_0, y_0)$.
2. Nahraj $(x_0, y_0)$ do frame buffera, teda zobraz bod $(x_0, y_0)$ do rastra.
3. Vypočítaj konštanty $dx$, $dy$, $2 dy$, $2(dy - dx)$ a urči hodnotu parametra $p_0$.
4. V každej z pozícii $x_i$ počnúc $i=0$ pozdĺž úsečky vykonaj test:
   1. Ak $p_i \lt 0$: nasledujúci bod je $(x_{i+1}, y_{i+1})=(x_i+1,y_i)$ a $p_{i+1}=p_i+2 dy$.
   2. Inak je nasledujúci bod $(x_{i+1}, y_{i+1})=(x_i+1,y_i+1)$ a $p_{i+1}=p_i+2 dy-2 dx$.
   3. Vykresli bod $(x_{i+1}, y_{i+1})$.
5. Opakuj krok 4. $dx$-krát.

Príklad

Na ilustráciu algoritmu si ukážeme rasterizáciu úsečky s krajnými bodmi $(x_A, y_A)=(0, 0)$ a $(x_B, y_B)=(7, 4)$.

1. Označíme $(x_0, y_0)=(x_A, y_A)=(0, 0)$
2. Zobrazíme tento bod do rastra.
3. $dx=7-0=7$, $dy=4-0=4$ (smernica $m=\frac{4}{7} \lt 1$ a teda sa priamka leží v I. oktante a riadiaca os je $x$), $2 dy=2.4=8$, $2(dy - dx)=2.(4-7)=-6$, $p_0=2.4-7=1$
   • $i=0:$ $p_0 \gt 0 \Rightarrow (x_1, y_1)=(x_0+1, y_0+1)=(1, 1)$ a $p_1=p_0+2(dy - dx) = -5$. Vykresli bod $(x_1, y_1)$.
   • $i=1:$ $p_1 \lt 0 \Rightarrow (x_2, y_2)=(x_1+1, y_1)=(2, 1)$ a $p_2=p_1+2dy = 3$. Vykresli bod $(x_2, y_2)$.
   • $i=2:$ $p_2 \gt 0 \Rightarrow (x_3, y_3)=(x_2+1, y_2+1)=(3, 2)$ a $p_3=p_2+2(dy - dx) = -3$. Vykresli bod $(x_3, y_3)$.
   • $i=3:$ $p_3 \lt 0 \Rightarrow (x_4, y_4)=(x_3+1, y_3)=(4, 2)$ a $p_4=p_3+2dy = 5$. Vykresli bod $(x_4, y_4)$.
   • $i=4:$ $p_4 \gt 0 \Rightarrow (x_5, y_5)=(x_4+1, y_4+1)=(5, 3)$ a $p_5=p_4+2(dy - dx) = -1$. Vykresli bod $(x_5, y_5)$.
   • $i=5:$ $p_5 \lt 0 \Rightarrow (x_6, y_6)=(x_5+1, y_5)=(6, 3)$ a $p_6=p_5+2dy = 7$. Vykresli bod $(x_6, y_6)$.
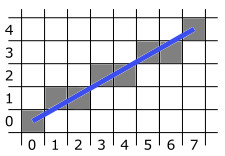
   • $i=6:$ $p_6 \gt 0 \Rightarrow (x_7, y_7)=(x_6+1, y_6+1)=(7, 4)$. Príkaz sme vykonali $dx$-krát a dostali sme sa do krajného bodu $(x_B, y_B)$. Vykresli bod $(x_7, y_7)$. Výsledok je zobrazený na Obr. 3.

Ďalšie riešené a neriešené príklady.

Interaktívny applet

Pseudokód

Implementácia Bresenhamovho algoritmu pre smernicu úsečky $0 \lt m \lt 1$ je zhrnutá v nasledujúcom pseudokóde. Na vstupe sú dva krajné body úsečky $A=(x_A,y_A)$ a $B=(x_B,y_B)$.

Literatúra

Bresenhamov algoritmus je podrobne spracovaný v literatúre [3] od strany 88. V slovenskej/českej literatúre ho nájdeme odvodený v [1] na strane 58 a taktiež v [2] od strany 82.