Počítačová grafika

DDA algoritmus (Digital Differential Analyzer Algorithm)

Princíp algoritmu

DDA algoritmus je rýchlejšia metóda pre výpočet polôh pixlov ako použiť smernicovú rovnicu priamky.

Nepoužívame pri ňom násobenie, ale výpočet súradníc pixlov pozdĺž priamky v reálnej aritmetike. Chyba zaokrúhlenia sa napriek tomu považuje za nepodstatnú.

DDA (Digital Differential Analyzer) je prírastkový algoritmus. Vychádza z rovnice $dy=m*dx$, ktorú dostaneme ako formálny prepis smernicovej rovnice priamky. Úsečka je krokovaná jednotkovým krokom v smere jednej z osí $x$ alebo $y$ a druhá súradnica sa vyjadrí zo smernice priamky $m=\frac{dy}{dx}$. Os, v ktorej smere prebieha vzorkovanie, sa nazýva riadiaca/hlavná os a druhá je vedlajšia os. Aby sme sa pri tomto postupe vyhli výskytu medzier na zobrazených úsečkách, nemôže zobrazovaná priamka prudko stúpať alebo klesať od riadiacej osi (Obr. 1). Ak tento prípad nastane, vymeníme úlohu súradnicových osí, t.j. jednotkové krokovanie budeme realizovať v smere druhej súradnicovej osi.

Nachádzame sa v bode úsečky $(x_i,y_i)$ a potrebujeme určiť nasledujúci bod $(x_{i+1},y_{i+1})$, ktorý vieme vyjadriť ako \begin{equation*} %s hviezdickou sa necisluje \begin{split} x_{i+1}=x_{i}+incr_x, \\ y_{i+1}=y_{i}+incr_y, \end{split} \end{equation*} kde $incr_x$ a $incr_y$ je prírastok (z ang. increment) v smere $x$ a $y$.

Uvažujme úsečku $AB$. Prípady, ktoré môžu nastať:

• Ak $|m| \lt 1\Rightarrow \mid dy\mid \lt \mid dx \mid$ a $x_A \lt x_B$ (bod $A$ sa nachádza vľavo od bodu $B$), tak úsečka má dominantný smer $x$. Vzorkovanie bude teda prebiehať v smere osi $x$ o konštantnú hodnotu +1. Hodnotu nasledujúcej $y$-ovej súradnice určíme zo smernicovej rovnice priamky ako $y_{i+1}=mx_{i+1}+b=m(x_{i}+1)+b=y_{i}+m]$. Teda platí \begin{equation*} %s hviezdickou sa necisluje \begin{split} x_{i+1}=x_{i}+1, \\ y_{i+1}=y_{i}+m. \end{split} \end{equation*}
• Ak $|m| \lt 1\Rightarrow \mid dy\mid \lt \mid dx \mid$ a $x_A>x_B$ (bod $A$ sa nachádza vpravo od bodu $B$), môžeme body $A$ a $B$ navzájom vymeniť alebo ekvivalentne postupovať tak, že položíme hodnotu $incr_x=-1$. Potom $y_{i+1}=my_{i+1}+b=m(x_{i}-1)+b=y_{i}-m$. Teda \begin{equation*} %s hviezdickou sa necisluje \begin{split} x_{i+1}=x_{i}+1, \\ y_{i+1}=y_{i}-m. \end{split} \end{equation*}
• Ak $|m| \gt 1\Rightarrow \mid dy\mid \gt \mid dx \mid$ a $y_A \lt y_B$ (bod $A$ sa nachádza nižšie ako bod $B$), tak úsečka má dominantný smer $y$. Vzorkovanie bude prebiehať v smere osi $y$ o konštantnú hodnotu +1. Hodnotu nasledujúcej $x$-ovej súradnice určíme zo smernicovej rovnice priamky ako $x_{i+1}=(y_{i+1}-b) \frac{1}{m}=(y_i+1-b) \frac{1}{m}=(mx_i+b+1-b) \frac{1}{m}=x_i+\frac{1}{m}$. Teda platí \begin{equation*} %s hviezdickou sa necisluje \begin{split} x_{i+1}=x_{i}+\frac{1}{m}, \\ y_{i+1}=y_{i}+1. \end{split} \end{equation*}
• Ak $|m| \gt 1\Rightarrow \mid dy\mid \gt \mid dx \mid$ a $x_A>x_B$ (bod $A$ sa nachádza vyššie ako bod $B$), môžeme body $A$ a $B$ navzájom vymeniť alebo ekvivalentne postupovať tak, že položíme hodnotu $incr_y=-1$. Potom $x_{i+1}=(y_{i+1}-b) \frac{1}{m}=(y_i-1-b) \frac{1}{m}=(mx_i+b-1-b) \frac{1}{m}=x_i-\frac{1}{m}$. Teda \begin{equation*} %s hviezdickou sa necisluje \begin{split} x_{i+1}=x_{i}-\frac{1}{m}, \\ y_{i+1}=y_{i}-1. \end{split} \end{equation*}

Je zrejmé, že počet vykreslených bodov v rastri pozdĺž úsečky sa rovná maximálnej hodnote rozdielu $x$/$y$-ovej súradnice krajných bodov, teda $n=max\lbrace\mid dy \mid,\mid dx \mid \rbrace$. Môžeme povedať, že pre $incr_x$ a $incr_y$ platí: \begin{equation*} incr_x=\frac{dx}{n} \\ incr_y=\frac{dy}{n} \end{equation*}

Postup výpočtu

1. Vlož dva krajné body $(x_A, y_A)$ a $(x_B, y_B)$ a zober ľavý (s menšou $x$-ovou súradnicou) ako bod $(x_0, y_0)$.
2. Nahraj $(x_0, y_0)$ do frame buffera, teda zobraz bod $(x_0, y_0)$ do rastra.
3. Vypočítaj konštanty $dx=x_B-x_A$, $dy=y_B-y_A$, $m=\frac{dy}{dx}$, $n=max\lbrace\mid dy \mid,\mid dx \mid \rbrace$ a hodnoty $incr_x=\frac{dx}{n}$, $incr_y=\frac{dy}{n}$ .
4. V každej pozícii $x_i$ počnúc $i=1$ až po $i=n$ pozdĺž úsečky vykonaj:
   1. $(x_{i+1}, y_{i+1})=(x_i+incr_x,y_i+incr_y)$.
   2. Zaokrúhli $(x_{i+1}, y_{i+1})$ na celé čísla.
   3. Vykresli bod $(x_{i+1},y_{i+1})$.

Príklad

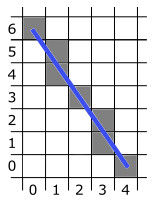
Na ilustráciu algoritmu si ukážeme rasterizáciu úsečky s krajnými bodmi $(x_A, y_A)=(0, 6)$ a $(x_B, y_B)=(4, 0)$.

1. Označíme $(x_0, y_0)=(x_A, y_A)=(0, 6)$
2. Zobrazíme tento bod do rastra.
3. $dx=4-0=4$,$dy=0-6=-6$, $m=\frac{-3}{2}$, $n=6$, $incr_x=\frac{2}{3}$, $incr_y=-1$
   • $i=1:$ $(x_1, y_1)=(x_0+incr_x, y_0+incr_y)=(\frac{2}{3}, 5)$. Zaokrúhlenie $(x_1, y_1)=(1,5)$. Vykresli bod $(x_1, y_1)$.
   • $i=2:$ $(x_2, y_2)=(x_1+incr_x, y_1+incr_y)=(\frac{4}{3}, 4)$. Zaokrúhlenie $(x_2, y_2)=(1,4)$. Vykresli bod $(x_2, y_2)$.
   • $i=3:$ $(x_3, y_3)=(x_2+incr_x, y_2+incr_y)=(\frac{6}{3}, 3)$. Zaokrúhlenie $(x_3, y_3)=(2,3)$. Vykresli bod $(x_3, y_3)$.
   • $i=4:$ $(x_4, y_4)=(x_3+incr_x, y_3+incr_y)=(\frac{8}{3}, 2)$. Zaokrúhlenie $(x_4, y_4)=(3,2)$. Vykresli bod $(x_4, y_4)$.
   • $i=5:$ $(x_5, y_5)=(x_4+incr_x, y_4+incr_y)=(\frac{10}{3},1)$. Zaokrúhlenie $(x_5, y_5)=(3,1)$. Vykresli bod $(x_5, y_5)$.
   • $i=6:$ $(x_6, y_6)=(x_5+incr_x, y_5+incr_y)=(\frac{12}{3}, 0)$. Zaokrúhlenie $(x_6, y_6)=(4,0)$. Vykresli bod $(x_6, y_6)$.Hodnota $i=n$ a dostali sme sa do koncového bodu $(x_B, y_B)$. Výsledok môžeme vidieť na Obr. 2.

Ďalšie riešené a neriešené príklady.

Interaktívny applet

Pseudokód

Implementácia DDA algoritmu je zhrnutá v nasledujúcom pseudokóde. Na vstupe sú krajné body úsečky. Parametre $dx$ a $dy$ predstavujú horizontálnu a vertikálnu vzdialenosť dvoch krajných bodov úsečky. Väčšia z týchto hodnôt určuje hodnotu parametru steps.

Ak absolútna hodnota $dx$ je väčšia ako absolútna hodnota $dy$ a $x_A$ je menšie ako $x_B$, hodnoty prírastku xIncrement a yIncrement sú 1 a $m$. V opačnom prípade, ak $x_A \gt x_B$, tak hodnoty prírastkov xIncrement a yIncrement sú -1 a $-m$.

Funkcia ROUND(x) predstavuje zaokrúhlenie hodnoty $x$ na celé čísla.

Literatúra

Algoritmus DDA vieme nájst’ podrobne spracovaný v anglickej literatúre [3] od strany 87. S jeho odvodením sa môžeme stretnút’ aj v [1] na strane 55 a je mu venovaná jedna strana 81 v [2].