Algoritmy na rasterizáciu kružnice

Kružnice sú často používané komponenty v obrázkoch a grafoch, a preto sú procedúry na ich generovanie zahrnuté v grafických knižniciach. Kružnica v $E^2$ je definovaná ako množina všetkých bodov v rovine, ktoré sú vo vzdialenosti $r$ od stredu kružnice $(x_C,y_C)$. Číslo $r$ nazývame polomerom kružnice.

Implicitnú rovnicu kružnice v karteziánskej súradnicovej sústave môžeme zapísať ako množinu bodov $(x,y)$, ktoré vyhovujú rovnici \begin{equation} (x-x_C)^2+(y-y_C)^2-r^2=0, \end{equation} kde $(x_C,y_C)$ je stred kružnice a $r$ je polomer danej kružnice.

Túto rovnicu je možné upraviť na explicitné vyjadrenie \begin{equation} y=y_C \pm \sqrt{r^2-(x_C-x)^2}, \end{equation} v ktorom môžeme využiť jednotkový krok na osi $x$, a $x\in\left\langle x_C-r,x_C+r\right\rangle$.

Táto metóda však nie je najvýhodnejšia pre generovanie kružníc. Problémom je veľa výpočtov v každom kroku a pri vykresľovaní sa objavujú medzery medzi jednotlivými pixelmi (Obr. 1).

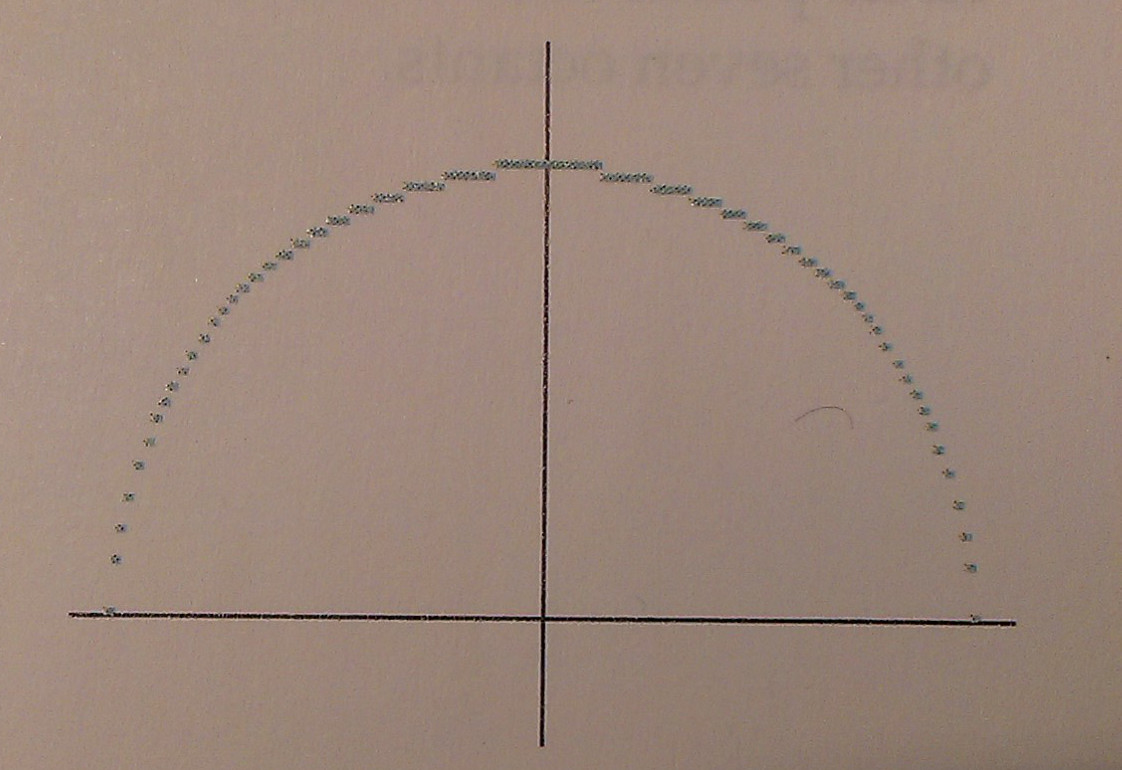
Obr. 1 - Kružnica vykreslená v kladnej polrovine pomocou rovnice implicitnej rovnice kružnice [3]

Môžeme zameniť úlohy $x$ a $y$ a postupovať jednotkovým krokom po $y$-ovej súradnici, čím však zvýšime počet potrebných výpočtov a predĺžime čas behu algoritmu. Určitú elimináciu nerovnomerne zobrazených pixlov (Obr. 1) môžeme zabezpečiť pomocou parametrizovaného vyjadrenia kružnice.

Parametrizovaná rovnica kružnice:

\begin{equation} \begin{split} x(t)=x_C+r.\cos(t), \\ y(t)=y_C+r.\sin(t), \end{split} \end{equation} kde parameter $t \in \left\langle 0,2 \pi\right)$, $r$ je polomer kružnice a $(x_C,y_C)$ je stred danej kružnice.

Ak generujeme kružnicu pomocou týchto rovníc pri rovnomernom uhlovom kroku, kružnica je zobrazená s rovnomerne vzdialenými bodmi pozdĺž kružnice. Väčšie medzery medzi bodmi kružnice môžu byť spojené úsečkami, aby aproximovali kružnicový tvar. Pre spojité zobrazenie kružnice môžeme použiť krokovanie o veľkosti $\frac{1}{r}$. Získané body následne budú vzdialené približne jeden pixel od seba.

Generovanie bodov kružnice môže byť zjednodušené využitím osových a stredových súmerností kružnice (Obr. 2).

Obr. 2 - Symetrie bodu $(x,y)$ na kružnici [3]

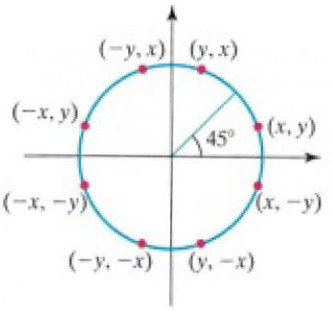
Segmenty kružnice sú v jednotlivých oktantoch 1-8 rovnaké. Preto stačí generovať iba segment kružnice v jednom oktante a ten pomocou súmerností zobraziť do ostatných.

Generovanie kružnice pomocou vyššie opísaných postupov vyžaduje značné množstvo výpočtov a teda dlhší čas behu algoritmu. V nasledujúcich podkapitolách opíšeme algoritmy na efektívne vykreslenie kružnice: minimalizácia výpočtov a s využitím len celočíselnej aritmetiky.

Medzi základné algoritmy rasterizácie kružnice patria dva algoritmy: Bresenhamov kružnicový algoritmus a Bresenhamov stredový kružnicový algoritmus. Pri všetkých algoritmoch máme na vstupe polomer $r$ a stred $(x_C,y_C)$ kružnice $K$. Na výstupe dostaneme množinu bodov rastra, ktoré aproximujú danú kružnicu $K$.