Počítačová grafika

Bresenhamov kružnicový algoritmus (Bresenham's Circle Algorithm)

Princíp algoritmu

Tento algoritmus predstavuje zovšeobecnenie Bresenhamovho algoritmu rasterizácie úsečky na kružnicu. Rozklad zrýchlime tým, že budeme generovať len segment kružnice v jednom oktante. Ostatné časti kružnice dostaneme súmernosťou podľa súradnicových osí $x$, $y$ a priamok $x=y$ a $y=-x$.

Výber pixlov je založený na rovnakom princípe ako pri úsečke, kde z dvoch možných kandidátov na vysvietenie vyberáme toho, ktorého stred je bližšie ku danej kružnici. Využívame parameter $p_i=d_1-d_2$, ktorý sa vyčísľuje rekurentne, kde hodnoty $d_1$ a $d_2$ sú štvorcami rozdielov $y$-ových súradníc.

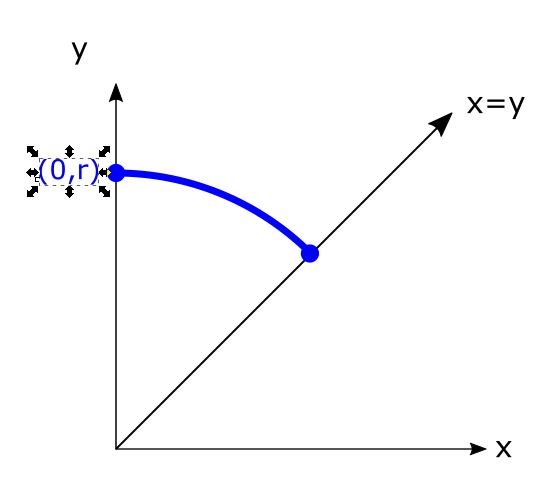
Pre ilustráciu algoritmu volíme kružnicu so stredom v začiatku súradnicovej sústavy a zobrazíme jej segment, ktorý sa začína v bode $(0,r)$ a končí, v bode $(x_i,y_i)$, kde $x_i \geq y_i$ (Obr. 1). V tomto prípade je jednotkový krok v smere súradnicovej osi $x$. Nachádzame sa v bode $(x_i,y_i)$ a potrebujeme sa rozhodnúť, ktorý z pixlov $E=(x_i+1,y_i)$ alebo $SE=(x_i+1,y_i-1)$ si vyberieme (Obr. 2).

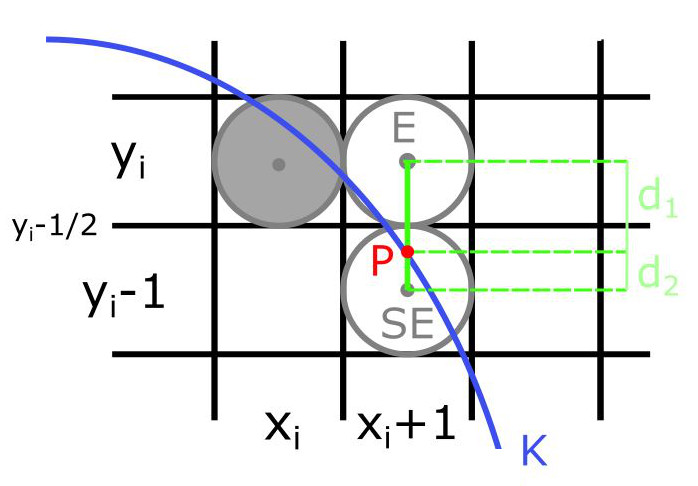
Označíme si $d_1={y_i^2}-y^2$ a $d_2=y^2-(y_i-1)^2$, kde $y$ je hodnota určená rovnicou $y^2=r^2-(x_i+1)^2$ z implicitnej rovnice kruznice. Hodnota $d_1$ vyjadruje vzdialenosť medzi bodmi $E$ a $(x_i+1,y)$ a hodnota $d_2$ medzi $(x_i+1,y)$ a $SE$. Určíme $p_i=d_1-d_2=2(x_i+1)^2+y_i^2+(y_i-1)^2-2r^2$. Zrejme platí

• Ak $p_i \lt 0 \Leftrightarrow d_1 \lt d_2$, tak bod $E$ je bližšie k bodu na kružnici $(x_i+1,y_i)$ a preto vysvietime pixel $E$.
• Ak $p_i \geq 0 \Leftrightarrow d_1\geq d_2$, tak je bližšie bod $SE$, ktorý následne vysvietime. Pri rovnosti môžeme vybrať ľubovoľný z bodov $E$, $SE$, no zvyčajne sa vyberá vyššie položený bod.

Teraz vyjadríme parameter $p_{i}$ rekurentne pomocou $p_{i+1}$

$p_{i+1}=2(x_{i+1}+1)^2+y_{i+1}^2+(y_{i+1}-1)^2-2r^2$ a rozdielu $p_{i+1}-p_i=4x_i+6+2(y_{i+1}^2-y_i^2)-2(y_{i+1}-y_i)$.

Možno zapísať rekurentný vzťah $p_{i+1}=p_i+4x_i+6+2(y_{i+1}^2-y_i^2)-2(y_{i+1}-y_i)$ Teda:

• Ak $p_i \lt 0 \Leftrightarrow d_1 \lt d_2$, nasledujúci bod je $(x_{i+1},y_{i+1})=E=(x_i+1,y_i)$ a $p_{i+1}=p_i+4x_i+6$
• Ak $p_i \geq 0 \Leftrightarrow d_1\geq d_2$, nasledujúci bod je $(x_{i+1},y_{i+1})=SE=(x_i+1,y_i-1)$, a preto $p_{i+1}=p_i+4x_i+6+2(y_i-y_i^2)$

Potom pre začiatočnú hodnotu $p_0$ v bode $(x_C,y_C)=(0,r)$ dostaneme $p_0=3-2r$. Hoci pri výpočte parametra sa používa násobenie, príslušný násobok je druhou mocninou a je možná implementácia cez logické operácie. Ostatné operácie sú celočíselné sčítanie a odčítanie.

Postup výpočtu

Kroky algoritmu vieme zhrnúť nasledovne:

1. Zadaj polomer $r$ a stred kružnice $(x_C,y_C)$ a urči prvý bod na kružnici so stredom v začiatku ako $(x_0 ,y_0)=(0, r)$.
2. Vypočítaj začiatočnú hodnotu rozhodovacieho parametra ako $p_0 =3-2r$
3. V každej pozícii $x_i$, štartujúc v $i=0$, vykonaj nasledujúci test:
   1. Ak $p_i \lt 0$: nasledujúci bod pozdĺž kružnice so stredom $(0,0)$ bude $(x_{i+1}, y_{i+1})=(x_i+1,y_i)$ a $p_{i+1}=p_i+4x_i+6$.
   2. Inak je nasledujúci bod $(x_{i+1}, y_{i+1})=(x_i+1,y_i-1)$ a $p_{i+1}=p_i+4(x_i-y_i)+10$.
4. Urči súmerne položené body v ostatných siedmich oktantoch.
5. Posuň každú vypočítanú pixlovú pozíciu $(x, y)$ na kružnicu so stredom $(x_C ,y_C )$ a zobraz bod so súradnicami: $x=x+x_C$,$y=y+y_C$.
6. Opakuj kroky 3. až 5. pokiaľ $x_i \geq y_i$.

Príklad

Na ilustráciu algoritmu si ukážeme rasterizáciu kružnice s polomerom $r=8$ a stredom kružnice $(x_C, y_C)=(1, 2)$.

1. $(x_0,y_0)=(0,r)=(0,8)$
2. $p_0=3-2r=-13$
3. • $i=0:~p_0 \lt 0 \Rightarrow (x_1,y_1)=(x_0+1,y_0)=(1,8)$ a $p_1=p_0+4x_0+6=-7$
   • $i=1:~p_1 \lt 0 \Rightarrow (x_2,y_2)=(x_1+1,y_1)=(2,8)$ a $p_2=p_1+4x_1+6=3$
   • $i=2:~p_2 \gt 0 \Rightarrow (x_3,y_3)=(x_2+1,y_2-1)=(3,7)$ a $p_3=p_2+4(x_2-y_2)+10=-11$
   • $i=3:~p_3 \lt 0 \Rightarrow (x_4,y_4)=(x_3+1,y_3)=(4,7)$ a $p_4=p_3+4x_3+6=7$
   • $i=4:~p_4 \gt 0 \Rightarrow (x_5,y_5)=(x_4+1,y_4-1)=(5,6)$ a $p_5=p_4+4(x_4-y_4)+10=5$
   • $i=5:~p_5 \gt 0 \Rightarrow (x_6,y_6)=(x_5+1,y_5-1)=(6,5)$ a $x_6\geq y_6$ teda algoritmus končí.
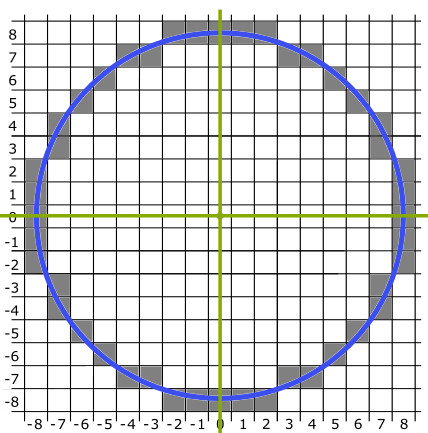
4. Určíme súmerne položené body v ostatných oktantoch (Obr. 3).
5. Posunieme každú hodnotu pixla do stredu $(1,2)$. Teda body: $(2,10),(3,10),(4,9),(5,9),(6,8), ...$

Ďalšie riešené a neriešené príklady.

Interaktívny applet

Pseudokód

Implementácia Bresenhamovho kružnicového algoritmu je zhrnutá v nasledujúcom pseudokóde. Na vstupe je stred $(x_C,y_C)$ a polomer kružnice $r$.

Literatúra

Bresenhamov kružnicový algoritmus sa nachádza podrobne spracovaný v literatúre [3]. Jeho myšlienka je načrtnutá aj v [1] na strane 62 a taktiež jeho vysvetlenie sa nachádza v [2] od strany 88.