Príklady
DDA algoritmus rasterizácie úsečky
-
Pomocou DDA algoritmu rasterizuj úsečku s krajnými bodmi $A=(-3, 2)$ a $B=(-6,6)$.
-
Rasterizuj úsečku s krajnými bodmi $A=(3,1)$ a $B=(-7,-1)$.
-
Rasterizuj úsečku s krajnými bodmi $A=(-2,1)$ a $B=(2,-2)$.
-
Rasterizuj orientovanú úsečku s krajnými bodmi $A=(-5,-4)$ a $B=(-2,6)$.
Rasterizuj úsečku s krajnými bodmi $A=(5,3)$ a $B=(4,1)$.
Prečo sa v DDA algoritme nepoužíva vždy jednotkové krokovanie v smere osi $x$? Ako sa problém rieši?
Kedy sa v algoritme DDA-line využíva rovnosť $x_{i+1}=x_i+\frac{1}{m}$ a kedy $x_{i+1}=x_i-\frac{1}{m}$? [11]
Bresenhamov algoritmus rasterizácie úsečky a Bresenhamov stredový algoritmus rasterizácie úsečky
-
Rasterizuj úsečku s krajnými bodmi $A=(-3, 2)$ a $B=(-6,6)$.
-
Odvoďte Bresenhamov algoritmus rasterizácie úsečky pre 5. oktant.
-
Uveďte Bresenhamov algoritmus na vykresľovanie úsečky v I. oktante (pseudokód + popis). [11]
-
Vyznač, ktoré časti rastra budú vysvietené Bresenhamovým algoritmomom pri rasterizácii úsečky so začiatočnými súradnicami $(1,1)$ a koncovými $(8,5)$. [11]
Rasterizuj úsečku s krajnými bodmi $A=(5,3)$ a $B=(4,1)$.
Pomocou Bresenhamovho algoritmu rozložte do rastra úsečku $AB$, kde $A=(1,2)$ a $B=(4,8)$.
Bresenhamov kružnicový algoritmus
-
Rasterizuj kružnicu so stredom v bode $(-1,-4)$ a polomerom $r=6$.
-
Modifikujte Bressenhamov kružnicový algoritmus pre I. oktant kružnice $k=\lbrace S,r\rbrace$. Vypočítajte súradnice obrazových bodov kružnice $k=\lbrace (0,0),10\rbrace$ ležiace v VIII. oktante.
-
Bresenhamovým algoritmom rozložte do rastra kružnicu $k:~x^2 + y^2 - 16 = 0$. Stačí I. oktant a začiatok nasledujúceho. [11]
-
Na čo slúži rovnosť: $p_{i+1}=p_i+4(x_i-y_i)+10$. Kedy a kde sa používa? Čo je $p_i$? [11]
-
Dokážte, že v Bressenhamovom algoritme pre kružnicu platí $p_{i+1}=p_i+4(x_i-y_i)+10$. [11]
-
Ako sú v Bressenhamovom algoritme pre kružnicu aproximované zvislé vzdialenosti, a ako je definovaný rozhodovací parameter $p_i$? Odvoďte $p_{i+1}$ pomocou $p_i$, ak viete, že $p_i \lt 0$. [11]
Bresenhamov stredový kružnicový algoritmus
-
Rasterizuj kružnicu so stredom v bode $(-5,0)$ a polomerom $r=10$.
Riadkový skenovací algoritmus alebo Scan line algoritmus
-
Rasterizuj pomocou scanline mnohouholník $A_{0}A_{1}A_{2}A_{3}A_{4}$, kde $A_{0}=(4,1)$, $A_{1}=(6,5)$, $A_{2}=(4,5)$, $A_{3}=(3,7)$, $A_{4}=(2,4)$. Použite priamku rovnobežnú so súradnicovou osou $y$.
-
Rasterizuj pomocou scanline mnohouholník $A_{0}A_{1}A_{2}A_{3}A_{4}$, kde $A_{0}=(1,1)$, $A_{1}=(5,0)$, $A_{2}=(7,2)$, $A_{3}=(5,6)$, $A_{4}=(3,5)$. Použite priamku rovnobežnú so súradnicovou osou $y$.
-
Napíšte rasterizáciu mnohouholníka $ABCDE$, kde $A=(4,1)$, $B=(6,5)$, $C=(4,5)$, $D=(3,7)$, $E=(2,4)$. Použite modifikovanýalgoritmus Scanline, ktorý používa skenovacie priamky rovnobežné s osou $y$ a zaokrúhľovanie round.
-
Rozložte do rastra trojuholník $ABC$, ak $A=(0,0)$, $B=(3,0)$, $C=(0,4)$. [11]
-
Rozložte do rastra úsečku $a=AB$, ak $A=(0,5)$ a $B=(5,0)$. [11]
-
Úsečka AB, kde $A=(3,2)$ a $B=(0,7)$ je neextremálna hrana mnohouholníka. Určte jej priesečníky so skanovacími priamkami a potom vykreslite jej rozklad do rastra pomocou Scan line algoritmu. [11]
Algoritmus Cohen-Sutherland
-
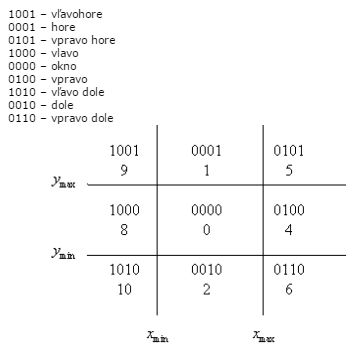
Orežte úsečky $AB$, $CD$ a $EF$ do okna určeného bodmi $P_1=(0,0)$, $P_2=(11,6)$ algoritmom Cohen-Sutherland, pričom $A=(4,0)$, $B=(12,8)$, $C=(-1,4)$, $D=(5,4)$, $E=(-3,2)$, $F=(5,-2)$.
-
Aké sú kroky Cohen–Sutherlandovho algoritmu (pseudokód). [11]
Algoritmus Liang-Barsky
-
Orež úsečku s krajnými bodmi $A=(0,3)$ a $B=(2,7)$ do mnohouholníka $A_{0}A_{1}A_{2}A_{3}A_{4}$, kde $A_{0}=(1,1)$, $A_{1}=(5,0)$, $A_{2}=(7,2)$, $A_{3}=(5,6)$, $A_{4}=(3,5)$.
-
Orež úsečku s krajnými bodmi $A=(3, 0)$ a $B=(6, 6)$ do mnohouholníka $A_{0}A_{1}A_{2}A_{3}A_{4}$, kde $A_{0}=(1,1)$, $A_{1}=(5,0)$, $A_{2}=(7,2)$, $A_{3}=(5,6)$, $A_{4}=(3,5)$.
-
Orežte úsečku $P_0 P_1$ trojuholníkom $ABC$, kde $P_0=(-5,3)$, $P_1=(5,3)$ a $A=(-4,4)$, $B=(4,4)$ a $C=(0,0)$.
-
Orezáva Cohen-Sutherlandov algoritmus úsečku aj v okolí bodu $B$ (koncový bod úsečky)? Ako sa rieši orezávanie v okolí $B$? [11]
-
Pomocou Liang-Barského algoritmu orežte úsečku $PQ$, kde $P=(0,8)$, $Q=(16,0)$ do okna určeného vrcholmi $A=(4,2)$, $B=(10,2)$, $C=(10,9)$ a $D=(4,9)$. [11]
-
Orežte úsečku $P_0 P_1$ do trojuholníka $ABC$ algoritmom Liang-Barsky, ak $P_0=(-3,6)$, $P_1=(3,6)$ a $A=(-4,4)$, $B=(4,4)$ a $C=(0,8)$. Použite vonkajšie normály.
Algoritmus Cyrus-Beck
-
Orežte úsečku $PQ$ lichobežníkom $STUW$, ak $S=(0,0)$, $T=(12,-2)$, $U=(7,3)$, $W=(4,4)$ a $P=(0,5)$, $Q=(8,-3)$.
-
V rovine je dané axiálne okno ľavým dolným $L=(3,2)$ a pravým horným rohom $P=(11,9)$ a orientovaná úsečka $AB$, kde $A=(0,7)$ a $B=(14,0)$. Orežte túto úsečku daným oknom algoritmom Cyrus-Beck. Orezávať začnite polrovinou $H_1= \langle L, \boldsymbol{e_L} = (-1, 0)\rangle$ a pokračujte proti smeru pohybu hodinových ručičiek polrovinami $H_2$, $H_3$, $H_4$.
-
Daná je úsečka $[(-2,-2),(0,5)]$ a orezávací obdĺžnik $[(-1,-1),(-1,1),(1,1),(1,-1)]$. Napíšte postup orezávania tohoto algoritmu pomocou Cyrus-Beck algorimu.
Viditeľnosť
-
Čo sú to zadné steny objektu a aká je podmienka na ich určenie? [11]
-
Na základe princípov objektovo orientovaného prístupu pre určovanie viditeľnosti určte viditeľnosť telesa $ABCDEFGH$ podobného kocke ak viete, že $A=(-3.5,3,4.5)$, $B=(0,10,2)$, $C=(6,9,7.5)$, $D=(4,2,9.5)$, $E=(-8,7,10)$, $F=(-4,14,8)$, $G=(3,13,13)$, $H=(-0.5,6,15)$ pri pohľade na teleso zdola v smere osi $z$-ovej. [11]
-
Daný je 2x2 pixel display. Použi Z-buffer na zistenie farby pre každý pixel daných objektov $A$ a $B$. $A$ – úsečka určená bodmi $(0.3,0,1.2)$ a $(2,2,0)]$. $B$ – štvorec určený $B_1=(0,0,1)$, $B_2=(2,0,1)$, $B_3=(2,2,1)$, $B_4=(0,2,1)$. [11]
-
Dané sú 3 úsečky $a$, $b$, $c$. Pomocou Maliarovho algoritmu zitite ich viditeľnosť, keď $a=[(1,2.5),(2.5,1)]$, $b=[(1,0.5),(2,1.5)]$, $c=[(1.5,2),(3,3)]$.
Iné
- S využitím rovníc otáčania so stredom v začiatku $O$ súradnicovej sústavy zapíšte v pseudokóde algoritmus pre vykreslenie pravidelného 6-uholníka so stredom v bode $O$ a dĺžkou strany $A=10$.
- Marek Juhár vo svojej diplomovej práci vytvoril v roku 2010 online interaktívne testy z počítačovej grafiky. K dispozícii sú príklady vo formáte, pdf prebrané z diplomovej práce. Hrubým písomom sú vyznačené správne odpovede